Ich werde mich an den Fall einer einfachen linearen Regression halten. Die Verallgemeinerung auf multiple Regression ist in den Prinzipien einfach, wenn auch in der Algebra hässlich. Stellen Sie sich vor, wir haben einige Werte eines Prädiktors oder einer erklärenden Variablen, $ x_i $, und wir beobachten die Werte der Antwortvariablen an diesen Punkten, $ y_i $. Wenn die wahre Beziehung linear ist und mein Modell korrekt angegeben ist (z. B. kein ausgelassener variabler Bias von anderen Prädiktoren, die ich vergessen habe), wurden diese $ y_i $ generiert aus:
$$ y_i = \ beta_0 + \ beta_1 x_i + \ epsilon_i $$
Jetzt ist $ \ epsilon_i $ ein zufälliger Fehler- oder Störungsterm, der beispielsweise $ \ mathcal {N hat } (0, \ sigma ^ 2) $ Verteilung. Diese Annahme der Normalität mit der gleichen Varianz ( Homoskedastizität) für jedes $ \ epsilon_i $ ist wichtig, damit all diese schönen Konfidenzintervalle und Signifikanztests funktionieren. Aus dem gleichen Grund gehe ich davon aus, dass $ \ epsilon_i $ und $ \ epsilon_j $ nicht korreliert sind, solange $ i \ neq j $ (wir müssen natürlich die unvermeidliche und harmlose Tatsache zulassen, dass $ \ epsilon_i $ perfekt korreliert ist mit sich selbst) - dies ist die Annahme, dass Störungen nicht autokorreliert sind.
Beachten Sie, dass wir nur $ x_i $ und $ y_i $ beobachten können, aber dass wir ' Ich sehe nicht direkt die $ \ epsilon_i $ und ihr $ \ sigma ^ 2 $ oder (interessanter für uns) die $ \ beta_0 $ und $ \ beta_1 $. Wir erhalten ( OLS oder "kleinste Quadrate") Schätzungen dieser Regressionsparameter $ \ hat {\ beta_0} $ und $ \ hat {\ beta_1} $, aber wir würden nicht erwarten, dass sie übereinstimmen $ \ beta_0 $ und $ \ beta_1 $ genau. Wenn ich weggehen und meinen Stichprobenvorgang wiederholen würde, würde ich selbst dann, wenn ich dieselben $ x_i $ 's wie die erste Stichprobe verwende, nicht dieselben $ y_i $' s erhalten - und daher meine Schätzungen $ \ hat {\ beta_0} $ und $ \ hat {\ beta_1} $ unterscheiden sich von zuvor. Dies liegt daran, dass ich bei jeder neuen Realisierung unterschiedliche Werte des Fehlers $ \ epsilon_i $ erhalte, die zu meinen $ y_i $ -Werten beitragen.
Die Tatsache, dass meine Regressionsschätzer bei jeder erneuten Abtastung anders aussehen, zeigt mir, dass sie einer Stichprobenverteilung folgen. Wenn Sie ein wenig statistische Theorie kennen, ist dies für Sie möglicherweise keine Überraschung - auch außerhalb des Regressionskontexts haben Schätzer Wahrscheinlichkeitsverteilungen, da es sich um Zufallsvariablen handelt, was wiederum darauf zurückzuführen ist, dass sie Funktionen von Beispieldaten sind, die selbst sind zufällig. Mit den oben aufgeführten Annahmen stellt sich heraus, dass:
$$ \ hat {\ beta_0} \ sim \ mathcal {N} \ left (\ beta_0, \, \ sigma ^ 2 \ left (\ frac) {1} {n} + \ frac {\ bar {x} ^ 2} {\ sum (X_i - \ bar {X}) ^ 2} \ right) \ right) $$
$$ \ hat {\ beta_1} \ sim \ mathcal {N} \ left (\ beta_1, \, \ frac {\ sigma ^ 2} {\ sum (X_i - \ bar {X}) ^ 2} \ right) $$
Es ist schön zu wissen, dass $ \ mathbb {E} (\ hat {\ beta_i}) = \ beta_i $, so dass "im Durchschnitt" meine Schätzungen mit den wahren Regressionskoeffizienten übereinstimmen (tatsächlich stimmt diese Tatsache nicht überein). Ich brauche nicht alle Annahmen, die ich zuvor getroffen habe - zum Beispiel spielt es keine Rolle, ob der Fehlerterm nicht normal verteilt ist oder ob sie heteroskedastisch sind, aber eine korrekte Modellspezifikation ohne Autokorrelation von Fehlern ist wichtig). Wenn ich viele Stichproben nehmen würde, würde der Durchschnitt der Schätzungen, die ich erhalte, gegen die wahren Parameter konvergieren. Sie werden dies vielleicht weniger beruhigend finden, wenn Sie sich daran erinnern, dass wir nur eine Probe sehen können! Aber die Unparteilichkeit unserer Schätzer ist eine gute Sache.
Interessant ist auch die Varianz. Im Wesentlichen ist dies ein Maß dafür, wie stark unsere Schätzer wahrscheinlich falsch liegen. Zum Beispiel wäre es sehr hilfreich, wenn wir ein $ z $ -Intervall konstruieren könnten, das uns sagen lässt, dass die Schätzung für den Steigungsparameter $ \ hat {\ beta_1} $, die wir aus einer Stichprobe erhalten würden, zu 95% wahrscheinlich ist liegen innerhalb von ungefähr $ \ pm 1.96 \ sqrt {\ frac {\ sigma ^ 2} {\ sum (X_i - \ bar {X}) ^ 2}} $ des wahren (aber unbekannten) Werts der Steigung, $ \ beta_1 $. Leider ist dies nicht so nützlich, wie wir es gerne hätten, da wir $ \ sigma ^ 2 $ nicht kennen. Es ist ein Parameter für die Varianz der gesamten Population zufälliger Fehler, und wir haben nur beobachtet eine endliche Stichprobe.
Wenn wir anstelle von $ \ sigma $ die Schätzung $ s $ verwenden, die wir aus unserer Stichprobe berechnet haben (verwirrenderweise wird dies oft als "Standardfehler der Regression" oder "Reststandard" bezeichnet Fehler ") Wir können den Standardfehler für unsere Schätzungen der Regressionskoeffizienten finden. Für $ \ hat {\ beta_1} $ wäre dies $ \ sqrt {\ frac {s ^ 2} {\ sum (X_i - \ bar {X}) ^ 2}} $. Da wir nun die Varianz einer normalverteilten Variablen schätzen mussten, müssen wir Student $ t $ anstelle von $ z $ verwenden, um Konfidenzintervalle zu bilden - wir verwenden die verbleibenden Freiheitsgrade von Die Regression, die in der einfachen linearen Regression $ n-2 $ beträgt, und für die multiple Regression subtrahieren wir einen weiteren Freiheitsgrad für jede zusätzliche geschätzte Steigung. Aber für einigermaßen große $ n $ und damit größere Freiheitsgrade gibt es keinen großen Unterschied zwischen $ t $ und $ z $. Faustregeln wie "Es besteht eine Wahrscheinlichkeit von 95%, dass der beobachtete Wert innerhalb von zwei Standardfehlern des korrekten Werts liegt" oder "Eine beobachtete Steigungsschätzung, die vier Standardfehler von Null entfernt ist, ist eindeutig statistisch hoch signifikant" funktioniert einwandfrei .
Ich finde, ein guter Weg, um Fehler zu verstehen, besteht darin, über die Umstände nachzudenken, unter denen ich erwarten würde, dass meine Regressionsschätzungen mehr (gut!) oder weniger (schlecht!) sind und wahrscheinlich nahe an den wahren Werten liegen. Angenommen, meine Daten waren "lauter", was passiert, wenn die Varianz der Fehlerterme $ \ sigma ^ 2 $ hoch war. (Ich kann das nicht direkt sehen, aber in meiner Regressionsausgabe würde ich wahrscheinlich feststellen, dass der Standardfehler der Regression hoch war.) Dann ist der größte Teil der Variation, die ich in $ y $ sehen kann, auf den zufälligen Fehler zurückzuführen. Dies maskiert das " -Signal" der Beziehung zwischen $ y $ und $ x $, was nun einen relativ kleinen Bruchteil der Variation erklärt und die Form dieser Beziehung schwieriger zu bestimmen macht. Beachten Sie, dass dies nicht bedeutet, dass ich die Steigung unterschätzen werde - wie ich bereits sagte, ist der Steigungsschätzer unvoreingenommen, und da er normal verteilt ist, unterschätze ich ihn wahrscheinlich genauso wie ich überschätzen. Da es jedoch schwieriger ist, die Beziehung aus dem Hintergrundgeräusch herauszusuchen, ist es wahrscheinlicher als zuvor, dass ich große Unterschätzungen oder große Überschätzungen mache. Mein Standardfehler hat zugenommen und meine geschätzten Regressionskoeffizienten sind weniger zuverlässig.
Intuition entspricht Algebra - beachten Sie, wie $ s ^ 2 $ im Zähler meines Standardfehlers für $ erscheint \ hat {\ beta_1} $. Wenn es also höher ist, ist die Verteilung von $ \ hat {\ beta_1} $ weiter verteilt. Dies bedeutet mehr Wahrscheinlichkeit in den Schwänzen (genau dort, wo ich es nicht will - dies entspricht Schätzungen, die weit vom wahren Wert entfernt sind) und weniger Wahrscheinlichkeit um den Peak (also weniger Wahrscheinlichkeit, dass sich die Steigungsschätzung in der Nähe der wahren Steigung befindet). Hier sind die Wahrscheinlichkeitsdichtekurven von $ \ hat {\ beta_1} $ mit hohem und niedrigem Standardfehler:
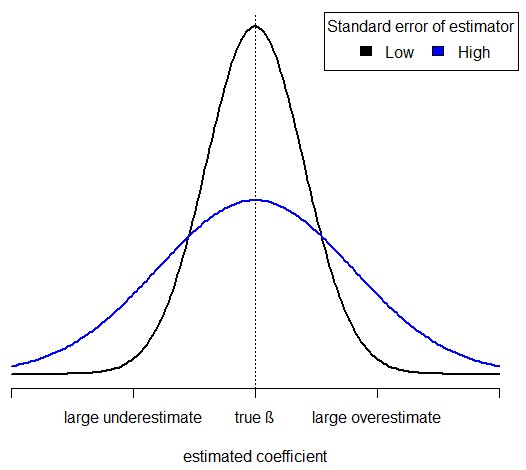
Es ist lehrreich, den Standardfehler von $ \ neu zu schreiben hat {\ beta_1} $ unter Verwendung der mittleren quadratischen Abweichung, $$ \ text {MSD} (x) = \ frac {1} {n} \ sum (x_i - \ bar {x}) ^ 2 $$
Dies ist ein Maß dafür, wie verteilt der Bereich der beobachteten $ x $ -Werte war. In diesem Sinne lautet der Standardfehler von $ \ hat {\ beta_1} $:
$$ \ text {se} (\ hat {\ beta_1}) = \ sqrt {\ frac {s ^ 2} {n \ text {MSD} (x)}} $$
Die Tatsache, dass $ n $ und $ \ text {MSD} (x) $ im Nenner stehen, bestätigt zwei weitere intuitive Fakten über unsere Unsicherheit. Wir können die Unsicherheit verringern, indem wir die Stichprobengröße erhöhen und gleichzeitig den Bereich der $ x $ -Werte, über die wir die Stichprobe erstellen, konstant halten. Wie immer ist dies mit Kosten verbunden - diese Quadratwurzel bedeutet, dass wir unsere Stichprobengröße vervierfachen müssen, um unsere Unsicherheit zu halbieren (eine Situation, die aus vielen Anwendungen außerhalb der Regression bekannt ist, z. B. Auswahl einer Stichprobengröße für politische Umfragen ). Es ist aber auch einfacher, den Trend von $ y $ gegenüber $ x $ zu erkennen, wenn wir unsere Beobachtungen auf einen größeren Bereich von $ x $ -Werten verteilen und damit die MSD erhöhen. Durch Vervierfachen der Streuung von $ x $ -Werten können wir unsere Unsicherheit in den Steigungsparametern halbieren.
Wenn Sie Ihre Stichprobengröße ausgewählt haben, haben Sie Schritte unternommen, um zufällige Fehler (z. B. aufgrund von Messfehlern) und möglicherweise zu reduzieren Sie entschieden sich für den Bereich der Prädiktorwerte, über die Sie eine Stichprobe erstellen würden, und hofften, die Unsicherheit in Ihren Regressionsschätzungen zu verringern. In dieser Hinsicht zeigen die Standardfehler an, wie erfolgreich Sie waren.
Ich füge Code für das Diagramm hinzu:
x <-seq (-5, 5, Länge = 200) y <-dnorm (x, Mittelwert = 0, sd = 1) y2 <-dnorm (x, Mittelwert = 0, sd = 2) Diagramm (x, y, Typ = "l", lwd = 2, Achsen = FALSE, xlab = "geschätzter Koeffizient", ylab = "") Linien (x, y2, lwd = 2, col = "blau") Achse (1, at = c (-5, -2,5, 0, 2,5,) 5), Labels = c ("", "große Unterschätzung", "wahres β", "große Überschätzung", "")) abline (v = 0, lty = "gepunktet") Legende ("topright", title = " Standardfehler des Schätzers ", c (" Niedrig "," Hoch "), Füllung = c (" Schwarz "," Blau "), Horizont = WAHR)