Wenn $ X_i $ iid Normal (0,1) sind, hat eine Stichprobe nur aufgrund zufälliger Abweichungen keinen Stichprobenmittelwert 0 oder keine Stichprobenstandardabweichung 1.

Überlegen Sie nun, was passiert, wenn wir $ Z = \ frac {X- \ overline {X}} {s_X} $

ausführen, während wir jetzt ausführen Haben Sie den Stichprobenmittelwert 0 und die Stichprobenstandardabweichung 1. Was wir nicht haben, ist, dass $ Z $ normal verteilt ist.

Bei kleinen bis mittleren Stichprobengrößen hat es kurze Schwänze. und wesentlich kleinere Kurtosis als ein Standardnormal. Tatsächlich sieht es aus der Simulation für Proben der Größe n = 10 einer skalierten Beta (4,4) ziemlich ähnlich aus (die so skaliert wurde, dass sie in (-3,3) liegt):

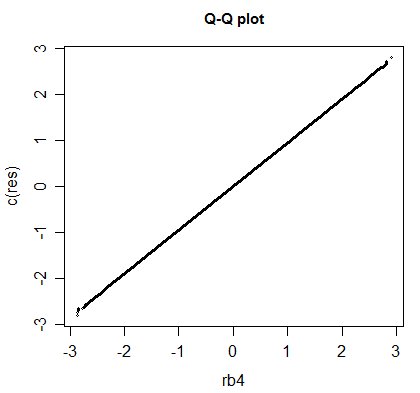
(Die x-Achse ist eine Zufallsstichprobe von B (4,4), skaliert auf (-3,3). Natürlich dies bedeutet nicht, dass die Verteilungsform eine Beta (4,4) ist.)

Die Werte in res wurden wie folgt generiert:

  res = replicate (100000, scale (rnorm (10)))  

Bei Stichproben der Größe 5 ähnelt das Ergebnis eher einer skalierten Beta (3 / 2,3 / 2).

Ferner sind die Werte in jeder Stichprobe nicht mehr unabhängig, da sie sich zu 0 summieren und ihre Quadrate zu $ ​​n-1 $

Wir haben das

$$ X_i ^ * = \ frac {X_i} {s} - \ frac {\ bar X} {s} $$

Die Stichprobenvarianz Aus einer normalen Stichprobe folgt eine genaue Verteilung.

$$ (n-1) s ^ 2 / \ sigma ^ 2 \ sim \ chi ^ 2_ {n-1} \ impliziert s ^ 2 \ sim \ frac {1} {n-1} \ chi ^ 2_ {n-1} \ impliziert s \ sim \ frac {1} {\ sqrt {n-1}} \ chi_ {n-1} $$

dh $ s $ folgt der Quadratwurzel eines Chi-Quadrats geteilt durch seine Freiheitsgrade.

Aber selbst wenn dies bedeutet, dass $ \ frac {X_i} {s} $ das Verhältnis einer Standardnormalen über ist Als Quadratwurzel eines Chi-Quadrats geteilt durch seine Freiheitsgrade ist der Zähler nicht unabhängig vom Nenner, und daher können wir nicht sagen, dass das Verhältnis der $ t $ -Verteilung eines Schülers (und persönlich) folgt Ich kenne seine Verteilung nicht.)

Für den zweiten Term ist bekannt, dass der Stichprobenmittelwert und die Stichprobenvarianz genau dann unabhängige Zufallsvariablen sind, wenn die Stichprobe aus unabhängigen Normalen besteht Fall hier.

Außerdem folgt der Stichprobenmittelwert einer Normalverteilung mit dem Mittelwert Null mit einer Varianz von hier $ 1 / n $, sodass $ \ sqrt {n} \ bar X $ einer Standardnormalen folgt.

Wir haben also $$ \ frac {\ sqrt {n} \ bar X} {s} \ sim t \ impliziert \ frac {\ bar X} {s} \ sim \ frac {1} {\ sqrt {n}} t $$

dh Der zweite Term von $ X_i ^ * $ folgt der $ t $ -Verteilung eines skalierten Schülers

Also insgesamt

$$ X ^ * _ i = \ frac {Z_i} {\ sqrt {\ chi ^ 2_ {n-1} / (n-1)}} - \ frac {1} {\ sqrt {n}} t $$

wobei I. haben das Symbol $ Z $ verwendet, um eine Zufallsvariable zu bezeichnen, die einer Standardnormalen folgt. Das erste Semester ist kein $ t $ eines Schülers und darüber hinaus nicht unabhängig vom zweiten Semester. Zusammengenommen sieht es auch nicht nach einer normalen oder einer Schülerverteilung aus.

Die ursprünglichen Standardnormalvariablen haben den WAHREN Mittelwert 0 (E (X) = 0) und sind unabhängig. Indem Sie einen Satz davon nehmen und durch ihre Standardabweichung dividieren, standardisieren Sie sie, aber das Ergebnis ist ironischerweise nicht normal. Sie sind abhängig (weil sie den Nenner teilen) und haben tatsächlich t-Verteilungen. Wenn Sie also Standard normal möchten, bleiben Sie einfach bei rnorm (5).

Habe gerade ein paar Experimente gemacht. Nach dem erneuten Skalieren scheinen Sie näher dran zu sein, um einige Daten mit $ \ mu = 0 $ und $ \ sigma = 1 $ zu erhalten.

  set.seed (123) x <norm (1000,0,1) Mittelwert (x) sd (x) y<-Skala (x) Mittelwert (y) sd (y)  

Ergebnisse:

  > Mittelwert (x) [1] 0,01612787> sd (x) [1] 0,991695> y<-Skala (x) > Mittelwert (x) y) [1] -8.235085e-18> sd (y) [1] 1  

Intuitiver Beweis durch Gegenbeispiel

Es gibt bereits einige allgemeine Antworten, die die Frage abdecken, aber ich persönlich finde die folgenden Überlegungen am einfachsten zu befolgen.

Angenommen, Ihre Stichprobengröße ist 1

Ihre Definition von $ X ^ * $ span> lautet wie folgt:

$$ X ^ * = \ frac {x- \ bar x} {sd (x)} $$ span>

Da die Stichprobengröße 1 ist, haben wir $ \ bar x = x $ span>, daher reduziert sich der Ausdruck für jeden $ x $ span> auf

$$ X ^ * = \ frac {\ bar x- \ bar x} {sd (x)} = \ frac {0} {0} $$ span>

Da $ X ^ * $ span> für Stichprobengröße 1 eindeutig nicht normal verteilt ist, kann es im Allgemeinen definitiv keine Standardnormalverteilung geben.