Als Antwort auf eine Frage in Kommentaren finden Sie hier einen Überblick über einige potenziell * schnellere Möglichkeiten, diskrete Verteilungen als die cdf-Methode durchzuführen.
* Ich sage "potenziell", weil in einigen diskreten Fällen ein Brunnen vorhanden ist Der implementierte inverse cdf-Ansatz kann sehr schnell sein. Der allgemeine Fall ist schwieriger zu lösen, ohne zusätzliche Tricks einzuführen.
Für den Fall von vier verschiedenen Ergebnissen wie im Beispiel in der Frage ist die naive Version des inversen cdf-Ansatzes (oder effektiv äquivalente Ansätze) fein; Aber wenn es Hunderte (oder Tausende oder Millionen) von Kategorien gibt, kann es langsam werden, ohne ein bisschen schlauer zu sein (Sie möchten auf keinen Fall sequentiell das PDF durchsuchen, bis Sie die erste Kategorie gefunden haben in dem das cdf eine zufällige Uniform überschreitet). Es gibt einige schnellere Ansätze als diesen.
[Sie können sehen, dass die ersten Dinge, die ich unten erwähne, eine Verbindung zu schneller als sequentiellen Ansätzen zum Auffinden eines Werts unter Verwendung eines Index haben und in gewisser Weise nur eine "intelligentere Version der Verwendung des cdf". Man kann sich natürlich "Standard" -Ansätze ansehen, um verwandte Probleme wie "Durchsuchen einer sortierten Datei" zu lösen, und Methoden erhalten, die viel schneller als die sequentielle Leistung sind. Wenn Sie geeignete Funktionen aufrufen können, sind solche Standardansätze häufig alles, was Sie benötigen.]
Auf jeden Fall einige effiziente Ansätze zum Generieren aus diskreten Verteilungen.
1 ) die "Tabellenmethode". Anstatt $ O (n) $ span> für $ n $ span> -Kategorien zu sein, wird die "einfache" "Version davon in (a) (wenn die Verteilung geeignet ist) ist $ O (1) $ span>.
a) Einfacher Ansatz - Annahme rationaler Wahrscheinlichkeiten (anhand des obigen Datenbeispiels):
- Richten Sie ein Array mit 10 Zellen ein, das eine '1', vier '2', zwei '3' und drei '4' enthält. Probieren Sie das mit einer diskreten Uniform (einfach aus einer kontinuierlichen Uniform), und Sie erhalten einfachen, schnellen Code.
b) Komplexerer Fall - benötigt keine 'netten' Wahrscheinlichkeiten. Verwenden Sie $ 2 ^ k $ span> -Zellen, oder Sie werden am Ende ein paar weniger verwenden. Betrachten Sie beispielsweise Folgendes:
x 0 1 2 3 4 5 6P (X = x) 0,4581 0,0032 0,1985 0,3298 0,0022 0,0080 0,0002
( Wir könnten natürlich 10000 Zellen haben und den vorherigen exakten Ansatz verwenden, aber was ist, wenn diese Wahrscheinlichkeiten beispielsweise irrational sind?)
Verwenden wir $ k = 8 $ span>. Multiplizieren Sie die Wahrscheinlichkeiten mit $ 2 ^ k $ span> und schneiden Sie sie ab, um herauszufinden, wie viele von jedem Zelltyp wir benötigen:
x 0 1 2 3 4 5 6 TotP (X = x) 0,4581 0,0032 0,1985 0,3298 0,0022 0,0080 0,0002 1,0000 [256p (x)] 117 0 50 84 0 2 0 253
Dann sind die letzten 3 Zellen im Grunde "Stattdessen aus dieser anderen Verteilung generieren" (dh p (x) - \ frac {\ lfloor 256 p (x) \ rfloor} {256}, normalisiert auf eine pmf):
x * 0 1 2 3 4 5 6 TotP (X = x *) 0,091200 0,273067 0,272000 0,142933 0,187733 0,016000 0,017067 1,000000
Die "Spillover" -Tabelle kann mit jeder vernünftigen Methode erstellt werden (Sie kommen nur in etwa 1% der Fälle hierher, sie muss nicht so schnell sein). $ \ frac {253} {256} $ span> der Zeit, in der wir eine zufällige Uniform erzeugen, verwenden Sie die ersten 8 Bits, um eine zufällige Zelle auszuwählen, und geben Sie den Wert in aus die Zelle; Nach der Ersteinrichtung kann dies alles sehr schnell erfolgen. Das andere $ \ frac {3} {256} $ span> der Zeit, in der wir eine Zelle mit der Aufschrift "Aus der zweiten Tabelle generieren" treffen. Fast immer generieren Sie eine einzelne Uniform auf $ (0,1) $ span> und erhalten eine diskrete Zufallszahl aus einer Multiplikation, einer Kürzung und den Kosten für den Zugriff auf ein Array-Element.
2) "Quadrieren des Histogramms" -Methode; Dies hängt irgendwie mit (1) zusammen, aber jede Zelle kann tatsächlich einen von zwei Werten erzeugen, abhängig von einer (kontinuierlichen) Uniform. Sie generieren also einen diskreten Wert von 1 bis n und prüfen dann in jedem Wert, ob der Hauptwert oder der zweite Wert generiert werden soll. Es funktioniert mit begrenzten Zufallsvariablen. Es gibt keine Spillover-Tabelle und es werden im Allgemeinen viel kleinere Tabellen als Methode (1) verwendet. Normalerweise ist es so eingerichtet, dass bei Auswahl von 1: n die ersten paar Bits einer einheitlichen Zufallszahl verwendet werden. Der Rest gibt an, welcher der beiden Werte für diesen Bin ausgegeben werden soll.
Vielleicht Der einfachste Weg, die Methode zu skizzieren, ist das obige Beispiel:
Stellen Sie sich die Verteilung als Histogramm mit 4 Fächern vor:
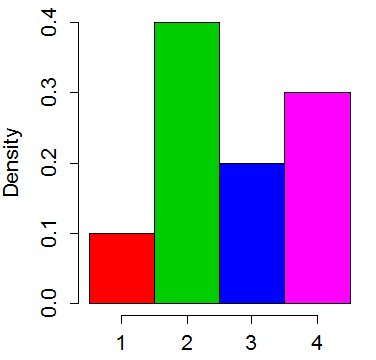
Wir schneiden die Spitzen der höchsten Balken ab und setzen sie in die kürzeren ein, um sie zu "quadrieren". Die durchschnittliche "Höhe" eines Balkens beträgt 0,25. Also schneiden wir 0,15 vom zweiten Balken ab und setzen ihn in den ersten und 0,05 vom vierten und setzen ihn in den dritten:
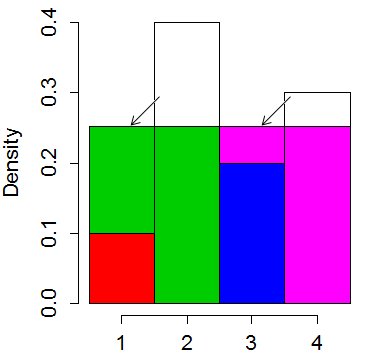
Es ist immer möglich, dies in zu organisieren Auf diese Weise erhält kein Behälter mehr als zwei Farben, obwohl eine Farbe in mehreren Behältern enden kann.
Nun wählen Sie zufällig einen der 4 Behälter aus (erfordert 2 zufällige Bits oben auf einer Uniform). Anschließend verwenden Sie die verbleibenden Bits, um eine gleichmäßig verteilte vertikale Position anzugeben und mit der Unterbrechung zwischen den Farben zu vergleichen, um herauszufinden, welcher der beiden Werte ausgegeben werden soll. Obwohl es sehr schnell ist, ist es normalerweise nicht ganz so schnell wie die 'table'-Methode.
-
Diese Methoden können angepasst werden, um mit unbegrenzten Variablen umzugehen, wobei es wiederum meistens schnell ist '.
Eine Referenz: http://www.jstatsoft.org/v11/i03/paper
Der relativ langsame Teil davon ist das Erstellen der Wertetabellen; Sie eignen sich, wenn Sie wissen, was Sie generieren werden ("Wir müssen in Zukunft viele Male Werte aus dieser Verteilung abtasten"), anstatt zu versuchen, sie im Laufe der Zeit zu erstellen. "Wir müssen eine Million Werte von diesem ASAP abtasten, aber wir werden es nie wieder tun müssen" schafft unterschiedliche Prioritäten; In vielen Situationen sind einige der "Standard-Computing-Ansätze" zum Nachschlagen sortierter Werte (dh zum schnelleren Ausführen der cdf-Methode) möglicherweise die beste Wahl.
Es gibt noch andere schnelle Ansätze aus diskreten Verteilungen zu erzeugen. Sorgfältig codiert können Sie eine sehr schnelle Generierung durchführen. Zum Beispiel:
3) Die Zurückweisungsmethode ("Akzeptieren-Zurückweisen") kann mit diskreten Verteilungen durchgeführt werden. Wenn Sie eine diskrete Majorisierungsfunktion ("Hüllkurve") haben, bei der es sich um eine vergrößerte diskrete PMF handelt, aus der Sie bereits schnell generieren können, passt sie sich direkt an und kann in einigen Fällen sehr schnell sein. Im Allgemeinen können Sie die Möglichkeit nutzen, aus kontinuierlichen Verteilungen zu generieren (z. B. indem Sie das Ergebnis zurück in eine diskrete Hüllkurve diskretisieren).
Stellen Sie sich hier vor, wir haben eine diskrete Wahrscheinlichkeitsfunktion $ f $ span>, für die wir kein geeignetes cdf (oder inverses cdf) haben - - In dieser Abbildung hatten wir nicht einmal die Normalisierungskonstante, daher ist unser Diagramm nicht normalisiert:
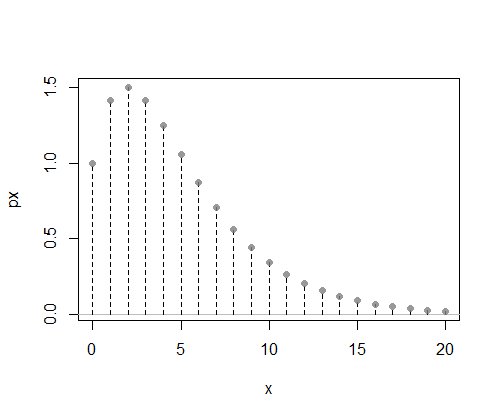
Nun müssen wir eine bequeme Funktion finden, die aus einer diskreten Wahrscheinlichkeitsfunktion $ g $ span> generiert werden kann, die mit einer Konstanten $ c $ span> und überall mindestens so groß wie $ f $ span> (wir müssen sicher sein, dass dies für alle $ x $ span> -Werte). Das heißt, $ cg (x) \ geq f (x) $ span> für alle möglichen $ x $ span> Werte.
Manchmal ist ein geeignetes $ g $ span> leicht zu identifizieren, aber eine nützliche Option besteht darin, eine Mischung aus einer diskreten Uniform für den linken Teil und zu nehmen eine Distribution mit mindestens so schwerem Schwanz wie $ f $ span> rechts. Zwei einigermaßen bequeme Möglichkeiten dafür sind eine geometrische Verteilung (wenn der Schwanz nicht langsamer als exponentiell abnimmt) und so etwas wie eine diskretisierte Pareto- oder diskretisierte Halb-Cauchy-Verteilung, die durch Nehmen von $ \ erhalten wird lfloor X \ rfloor $ span> für eine Pareto- oder Halb-Cauchy-Zufallsvariable $ X $ span> (in beiden Fällen, wenn die pmf langsamer als exponentiell abnimmt).
(In diesem Fall kann die Geometrie selbst durch Diskretisierung eines Exponentials erzeugt werden.)
In diesem Fall funktionieren eine diskrete Uniform links und eine Geometrie rechts recht gut :
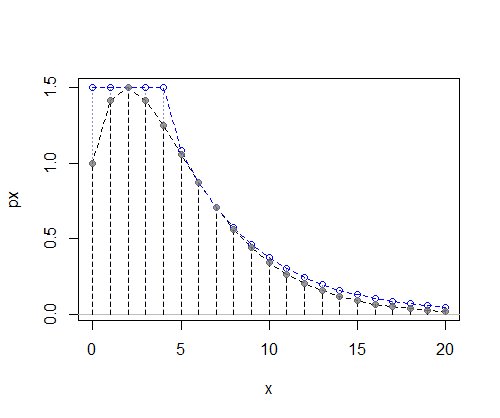
(Erinnerung: Was hier dargestellt ist, ist eine nicht normalisierte pmf, sodass die y-Achse keine Wahrscheinlichkeit darstellt, sondern etwas Proportionales zur Wahrscheinlichkeit)
Dann geht es bei der Prozedur darum, einen vorgeschlagenen Wert $ x $ span> aus $ g $ span> zu simulieren. Simulation einer Uniform, $ U $ span> auf $ (0, cg (x)) $ span> und wenn $ U<f $ span>, wobei das vorgeschlagene $ x $ span> akzeptiert wird (andernfalls wird es abgelehnt und ein neues vorgeschlagenes $ x $ span>).