Entschuldigung, ein bisschen neu hier, bitte entschuldigen Sie, wenn dies nicht allzu viel hilft.

Die US-amerikanische Sozialversicherungsbehörde führt Aufzeichnungen über Geburten und Todesfälle und stellt ihre Informationen zum Kauf zur Verfügung (anscheinend für ein hoher Preis): Hier

Ich habe jedoch eine Quelle gefunden, die behauptet, sie gekauft zu haben und sie kostenlos anbietet (sowie die nach Datum sortierten Daten auf der Website anbietet ): Hier

Ich gehe davon aus, dass Sie dies einfach als Beispiel verwenden und alle Daten mit einem Skript durchgehen können, um herauszufinden, wie viele Menschen an ihrem Geburtstag tatsächlich sterben. Ich würde das selbst tun, aber ich habe noch 20 Minuten zum Herunterladen (sie sind ungefähr 1,5 GB), also werde ich versuchen, mich selbst mit den Statistiken zu befassen, wenn ich die Zeit finde, ein Skript zu schreiben.

Natürlich können die Vereinigten Staaten nicht die gesamte Weltbevölkerung repräsentieren, aber es ist ein guter Anfang. Ich gehe davon aus, dass Sie an Geburtstagen aufgrund von "Problemen der ersten Welt" eine höhere Rate an Todesfällen sehen werden, weil wir die Vereinigten Staaten nutzen und ich denke, dass der Effekt auf der ganzen Welt weniger sichtbar wäre ...

Update - Nummern: D

Ich habe die Todesstammdatei der sozialen Sicherheit aus der kostenlosen Quelle durchgesehen, sodass ich nicht wissen kann, ob die Informationen gültig sind. Angesichts der Größe von jeweils ~ 3 Gigabyte und der Tatsache, dass niemand diese Art von Dateien fälschen kann, gehe ich davon aus, dass sie gültig sind.

Sie können den Code sehen, der Ich habe es hier durchgearbeitet: http://pastebin.com/9wUFuvpN

Es ist in C # geschrieben und liest die Zeilen des Todesindex nacheinander durch analysiert das Datum mit Regex. Ich nahm an, dass die Datei im Grunde genommen dieses Format hatte:

  `(Sozialversicherungsnummer) (Vorname) (Nachname) (zweiter Vorname) (ein Buchstabe) (MM-TT-JJJJ des Todes) (MM-TT-JJJJ der Geburt) ` 

Ich hatte Regex, habe nur den letzten Teil für das Geburts- / Sterbedatum ausgewählt und überprüft, ob eines der Felder nur 0 ist (was meiner Meinung nach bedeutet, dass die Sozialversicherung keinen gültigen Monat / Datum für bekommen konnte den Datensatz) und verwerfen Sie die Nullen. Dann wird geprüft, ob der Tag der Geburt und der Monat der Geburt mit dem Tag des Todes / dem Monat des Todes übereinstimmen, und dies wird zur Anzahl der am Geburtstag Verstorbenen hinzugefügt. Es werden alle Datensätze, die keine Nullen sind, zur Anzahl der Todesfälle hinzugefügt.

Die Ergebnisse werden in diesem Format ausgegeben:

Todesfälle am Geburtstag / Durchgesehene Todesfallzeilen - Personen mit einer 0 in einem ihrer Datensätze

Es ist großartig, wenn jemand diesen Code überprüfen kann, da ich einige Fehler gefunden habe, die ich zuvor gemacht habe und nur feststellen konnte weil meine Ergebnisse keinen statistischen Sinn ergaben.

Hier ist die Konsolenausgabe: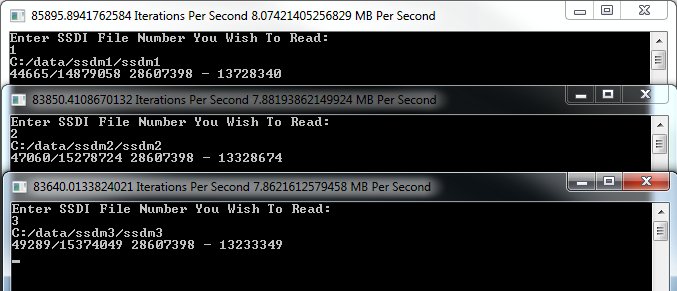

Rechnen ...

• Datei 1 hatte 44665 Todesfälle an einem Geburtstag von 14879058 Todesfälle insgesamt
• Datei 2 hatte 47060 Todesfälle an einem Geburtstag von 15278724 Todesfälle insgesamt
• Datei 3 hatte 49289 Todesfälle an einem Geburtstag von 15374049 Todesfälle insgesamt
• Insgesamt haben wir 141014 Todesfälle an einem Geburtstag von 45531831.

Wir haben also eine statistische Wahrscheinlichkeit von ~ 0,3097%, an einem Geburtstag zu sterben (1 /) 365) würde uns glauben machen, dass es nur eine ~ 0,27397% ige Chance gibt, an einem Geburtstag zu sterben. Das ist in der Tat eine 13% ige Erhöhung der Sterbewahrscheinlichkeit an einem Geburtstag von 1/365. Natürlich ist diese Stichprobe nur für Amerikaner und hat nur 45 Millionen Datensätze. Ich bin sicher, dass Organisationen, die ihre Arbeit ursprünglich veröffentlicht haben, Zugang zu viel zuverlässigeren und größeren Todesindizes hatten. Ich denke jedoch, dass es in der Tat gültig ist, dass Todesfälle an einem Geburtstag wahrscheinlicher sind als Todesfälle an einem anderen Tag.

Hier ist ein Zeitartikel, in dem Sprünge in Todesgründen an Geburtstagen genannt werden: Artikel

Bearbeiten 2: @cbeleites wies darauf hin, dass ich vergessen habe, Todesfälle am selben Tag zu berücksichtigen, was ein großer Faktor für die Zunahme der Todesfälle an Geburtstagen wäre. Genau genommen sind meine Daten immer noch gültig, aber ich habe sie nicht weggeworfen, wenn eine Person am selben Tag gestorben ist, an dem sie geboren wurde. Es ist interessant, dass meine Ergebnisse nicht zu stark von diesem Fehler betroffen waren. Es scheint also, dass diese Aufzeichnungen den Tod am ersten Tag nicht enthalten. Ich werde später darauf eingehen. Ich denke, es gibt sehr interessante Statistiken, nach denen ich suchen kann, wie zum Beispiel den Tod an Tagen im Monat und eine Art Heatmap. Ich werde das wahrscheinlich irgendwann versuchen ...

Wir können noch genauer sein als die Daten von @Mike Shi: Der gefährlichste aller Geburtstage ist der allererste.

Die dort gemeldeten Sterblichkeitsraten am ersten Tag liegen herum 0,2% für Industrieländer und 0,8% Durchschnitt für alle Länder. Dies bedeutet, dass das Sterberisiko am Tag der Geburt mindestens so hoch ist wie das Sterberisiko an jedem der folgenden Geburtstage *.

* Ich denke, es ist eine sichere Annahme, dass Todesfälle am ersten Tag nicht in der Akte von @Mark Shi erscheinen, da die Sterblichkeitsrate am ersten Tag in den USA bei 0,3% liegt ( andere Quelle: 0,26%)). Welches ist fast die gesamte Sterblichkeitsrate am Geburtstag in der Sozialversicherungsakte. Entweder erhalten Babys, die am Tag der Geburt sterben, keine Sozialversicherungsnummer, oder das Sterben an einem Geburtstag> 1 Jahr ist äußerst unwahrscheinlich.

Randnotiz:
Es gibt andere Tage wie Chirstmas und Silvester, von denen bekannt ist, dass sie ebenfalls überdurchschnittlich hohe Sterblichkeitsraten aufweisen.

Hier ist ein Argument, warum die Wahrscheinlichkeit des Todes am Geburtstag höher sein kann als an anderen Tagen: Geburtstage sind emotional aufgeladene Tage. Darüber hinaus neigen die Menschen dazu, es irgendwie zu feiern. Es gibt also einen Überschuss an Faktoren (im Verhältnis zum üblichen Lebensstil der Person), die den biologischen Stress erhöhen (übermäßige Emotionen, übermäßiges Trinken, übermäßiges Essen, übermäßiges Tanzen, übermäßiges Banjee-Springen usw.). Statistisch gesehen erhöht diese Situation die Wahrscheinlichkeit, an einem Geburtstag zu sterben, da sie alle gesundheitlichen Probleme einer Person verschärft oder die Person Situationen und Risiken aussetzt, für die die Person unerfahren ist.

Die Wahrscheinlichkeit, dass ein Neugeborenes innerhalb eines Jahres stirbt, finden Sie in den Lebenstabellen. Sie können beispielsweise die periodischen Lebenstabellen überprüfen und in der Spalte $ q_x $ nach $ x = 0 $ in der Datenbank zur menschlichen Sterblichkeit suchen. Dies ist nicht genau das, was Sie wollen, aber es wird Ihnen eine Idee geben.

Zusätzlich zu den anderen hervorragenden Antworten, aber es gibt einen Punkt, über den keiner gesprochen hat: Geburtstage sind nicht gleichmäßig über das Jahr verteilt, und Todestage sind es auch nicht. Das verschwört sich so, dass die "statistische" Wahrscheinlichkeit not 1/365 ist. Um eine Vorstellung von diesem Effekt zu bekommen, nehmen wir zunächst an, dass beide nahezu einheitlich sind. Nur der 29. Februar hat eine Wahrscheinlichkeit von 1/4 der anderen. Das gibt $$ 365 p + \ frac14 p = 1 $$ span> also $ p = 0,002737851 $ span>. Dies führt zu einer Wahrscheinlichkeit von Geburt und Tod am selben Tag, die gleich $ 356 \ cdot p ^ 2 + (p / 4) ^ 2 = 0,002736445 > 0,00273224 = \ frac1 {366} $ ist span> das ist der minimal mögliche Wert (mit 366 Tagen).

Mit etwas mehr Allgemeinheit sei $ p_i, i = 1, \ dotsc, n $ span> die Geburtstagswahrscheinlichkeiten und $ q_i, i = 1, \ dotsc, n $ span> die Todeswahrscheinlichkeiten für ein Jahr mit $ n $ span> Tagen. Wenn dann Geburtstag und Todestag für eine Person statistisch unabhängig sind, werden wir das feststellen $$ \ DeclareMathOperator {\ P} {\ mathbb {P}} \ P (\ text {Geburt und Tod am selben Tag}) = \ sum_ {i = 1} ^ n p_i q_i $$ span> Wenn also $ p_i = q_i $ span>, dann ist das $ \ sum_i p_i ^ 2 $ span>. Dies ist eine Größe, die (in der Biologie) als Simpsons Index der (Bio-) Diversität bekannt ist. Die Umkehrung könnte dann als "effektive Anzahl von Tagen (in einem Jahr)" angesehen werden! Der Mindestwert von $ \ sum_i p_i ^ 2 $ span> ist $ 1 / n $ span>. Um dies zu sehen, verwenden Sie Konvexität.

Unter der Annahme, dass $ p_i = q_i $ span> eine ziemliche Strecke ist, schauen wir uns zunächst einige Daten und Geburtstagswahrscheinlichkeiten für Norwegen an, die aus Daten von ssb.no: berechnet wurden. p>

Offensichtlich nicht einheitlich, der hohe Ausreißer ist der 1. Juli. Das ist nicht real, es wird von Einwanderern ohne dokumentierten Geburtstag verursacht, der an diesem Datum registriert wurde. Ein Maximum im Frühjahr, gegen Anfang April, ein weiteres Maximum im Herbst, im September. Der daraus berechnete Simpson-Index ist $ 0.002750224 $ span>, und die Umkehrung ist $ 363.6067 $ span>, also der "effektiv" Anzahl der Geburtstage "ist ungefähr 363 und eine halbe, ziemlich nahe bei 366. Die Ungleichmäßigkeit ist also vielleicht nicht zu wichtig. Es ist schwieriger, Daten für den Todestag zu finden, aber ich fand die Zeitung (auf Norwegisch) (dies ist das offizielle Journal der norwegischen Ärztekammer), die im Winter eine um 12% höhere Sterblichkeitsrate aufweist als im Sommer. Sie berichten auch über ein leicht erhöhtes Todesrisiko am Montag! Tatsächlich zeigen internationale Vergleiche, die von diesem Papier berichtet wurden, dass die Übersterblichkeit im Winter in Skandinavien am niedrigsten ist, in Ländern wie Irland oder England etwa doppelt so hoch. Das könnte überraschend sein, könnte es damit zu tun haben, dass wir Skandinavier wärmere und besser isolierte Häuser haben?

Daraus können wir eine Deathday-Verteilung rekonstruieren. Ich nehme den Winter ein halbes Jahr als November-April. Dann können wir rechnen $$ p_w = 1,12 p_s \\ (182 \ cdot 1.12 + 184) p_s = 1 $$ span> Dies führt zu $ p_s = 0,002578383, p_w = 0,002887789 $ span> und schließlich $ \ sum_i p_i q_i = 0,00273151 $ span>, seine Umkehrung, die "effektive Anzahl von Tagen" ist 366,1, ziemlich nahe bei 366! Die Antikorrelation ( $ \ rho (p_i, q_i) = - 0,06 $ span>) scheint die Ungleichmäßigkeit so auszugleichen, dass wir auch von Gleichmäßigkeit (und gleicher Verteilung) ausgehen können zum Geburtstag und Todestag). Das ist ziemlich interessant.

BEARBEITEN: Hier ist ein veröffentlichtes Papier zur Ungleichmäßigkeit des Geburtstagsproblems.

1 von 365 wäre die richtige Quote, da Sie garantiert an einem Tag eines 365-Tage-Jahres sterben ... Daher ist die Quote 1 von 365.