Ich fand die Antwort von BruceET interessant, was die Anzahl der Ereignisse betrifft. Eine alternative Möglichkeit, dieses Problem anzugehen, besteht darin, die Entsprechung zwischen Wartezeit und Anzahl der Ereignisse zu verwenden. Die Verwendung davon wäre, dass das Problem auf einige Arten leichter verallgemeinert werden kann.
Anzeigen des Problems als Wartezeitproblem
Diese Korrespondenz, wie zum Beispiel hier und hier erklärt / verwendet, ist
Für die Anzahl der Würfelwürfe $ m $ span> und die Anzahl der Treffer / Ereignisse $ k $ span> Sie bekommen:
$$ \ begin {array} {ccc}
\ overbrace {P (K \ geq k | m)} ^ {\ text {das ist, wonach Sie suchen}} & = &
\ overbrace {P (M \ leq m | k)} ^ {\ text {wir werden dies stattdessen ausdrücken}} \\
{\ small \ text {$ \ mathbb {P} $ $ k $ oder mehr Ereignisse in $ m $ Würfelwürfen}} & = & {\ small \ text {$ \ mathbb {P} $ Würfelwürfe unter $ m $ angegeben $ k $ events}}
\ end {array}
$$ span>
In Worten: Die Wahrscheinlichkeit, mehr als $ K \ geq k $ span> -Ereignisse zu erhalten (z. B. $ \ geq 1 $ span> mal 6) innerhalb einer Anzahl von Würfeln $ m $ span> entspricht der Wahrscheinlichkeit, $ m $ oder weniger Würfelwürfe, um $ k $ span> solche Ereignisse zu erhalten.
Dieser Ansatz bezieht sich auf viele Verteilungen.
Verteilung der Verteilung von
Wartezeit zwischen Ereignissen Anzahl der Ereignisse
Exponentielle Poisson
Erlang / Gamma über / unterdisperses Poisson
Geometrisches Binomial
Negatives Binomial über / unterdisperses Binomial
In unserer Situation ist die Wartezeit also eine geometrische Verteilung. Die Wahrscheinlichkeit, dass die Anzahl der Würfelwürfe $ M $ span>, bevor Sie den ersten $ n $ span> würfeln, geringer ist als oder gleich $ m $ span> (und mit einer Wahrscheinlichkeit, $ n $ span> zu würfeln, entspricht $ 1 / n $ span>) ist die folgende CDF für die geometrische Verteilung:
$$ P (M \ leq m) = 1- \ left (1- \ frac {1} {n} \ right) ^ m $$ span>
und wir suchen nach der Situation $ m = n $ span>, damit Sie Folgendes erhalten:
$$ P (\ text {innerhalb von $ n $ roll wird ein $ n $ gewürfelt}) = P (M \ leq n) = 1- \ left (1 - \ frac {1} {n} \ right) ^ n $$ span>
Verallgemeinerungen, wenn $ n \ bis \ infty $ span>
Die erste Verallgemeinerung ist, dass für $ n \ bis \ infty $ span> die Verteilung der Anzahl der Ereignisse zu Poisson mit dem Faktor $ \ lambda $ span> und die Wartezeit wird zu einer Exponentialverteilung mit dem Faktor $ \ lambda $ span>. Die Wartezeit für das Würfeln eines Ereignisses im Poisson-Würfelwurfprozess wird also zu $ (1-e ^ {- \ lambda \ times t}) $ span> und mit $ t = 1 $ span> Wir erhalten das gleiche $ \ ca. 0,632 $ span> -Ergebnis wie die anderen Antworten. Diese Verallgemeinerung ist noch nicht so speziell, da sie nur die anderen Ergebnisse wiedergibt, aber für die nächste sehe ich nicht so direkt, wie die Verallgemeinerung funktionieren könnte, ohne über Wartezeiten nachzudenken.
Verallgemeinerungen, wenn Würfel nicht fair sind
Sie könnten die Situation in Betracht ziehen, in der die Würfel nicht fair sind. Zum Beispiel würfeln Sie einmal mit einem Würfel mit einer Wahrscheinlichkeit von 0,17, eine 6 zu würfeln, und ein anderes Mal mit einem Würfel mit einer Wahrscheinlichkeit von 0,16, eine 6 zu würfeln und dass die Wahrscheinlichkeit, eine 6 in 6 Runden zu würfeln, geringer ist als die Zahl $ 1-1 / e $ span>. (Dies bedeutet, dass Sie basierend auf der durchschnittlichen Wahrscheinlichkeit eines einzelnen Wurfs, beispielsweise wenn Sie ihn aus einer Stichprobe vieler Würfe ermittelt haben, die Wahrscheinlichkeit in vielen Würfeln mit denselben Würfeln nicht bestimmen können, da Sie die Korrelation des Würfels berücksichtigen müssen Würfel)
Angenommen, ein Würfel hat keine konstante Wahrscheinlichkeit $ p = 1 / n $ span>, sondern wird aus einer Beta-Verteilung mit einer mittleren $ \ bar {p} = 1 / n $ span> und einige Formparameter $ \ nu $ span>
$$ p \ sim Beta \ left (\ alpha = \ nu \ frac {1} {n}, \ beta = \ nu \ frac {n-1} {n } \ right) $$ span>
Dann wird die Anzahl der Ereignisse für einen bestimmten Würfel, der $ n $ span> Zeit gewürfelt wird, Beta-Binomial verteilt. Die Wahrscheinlichkeit für ein oder mehrere Ereignisse ist:
$$ P (k \ geq 1) = 1 - \ frac {B (\ alpha, n + \ beta)} {B (\ alpha, \ beta)} = 1 - \ frac {B (\ nu \ frac {1} {n}, n + \ nu \ frac {n-1} {n})} {B (\ nu \ frac {1} {n}, n + \ nu \ frac {n-1} {n})} $$ span>
Ich kann rechnerisch überprüfen, ob dies funktioniert ...
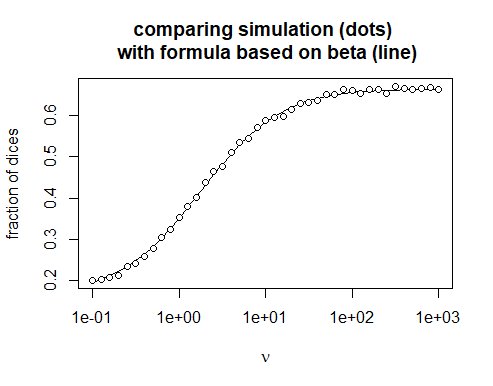
### Berechnen Sie das Ergebnis für das n-malige Werfen eines n-seitigen Würfels
rolldice <- Funktion (n, nu) {
p <rbeta (1, nu * 1 / n, nu * (n-1) / n)
k <rbinom (1, n, p)
aus <- (k>0)
aus
}}
### Berechnen Sie den Durchschnitt für eine Würfelprobe
Meandice <-Funktion (n, nu, reps = 10 ^ 4) {
Summe (replizieren (Wiederholungen, Würfeln (n, nu))) / Wiederholungen
}}
Meandice <-Vectorize ((Meandice))
### simulieren und berechnen für Varianz n
set.seed (1)
n <- 6
nu <-10 ^ seq (-1,3,0,1)
y <-meandice (n, nu)
Diagramm (nu, 1-beta (nu * 1 / n, n + nu * (n-1) / n) / beta (nu * 1 / n, nu * (n-1) / n), log = "x ", xlab = Ausdruck (nu), ylab =" Bruchteil der Würfel ",
main = "Simulation (Punkte) vergleichen \ n mit Formel basierend auf Beta (Linie)", main.cex = 1, type = "l")
Punkte (nu, y, lty = 1, pch = 21, col = "schwarz", bg = "weiß")
.... Aber ich habe keine gute Möglichkeit, den Ausdruck für $ n \ to \ infty $ span> analytisch zu lösen.
Wmit der Wartezeit Mit Wartezeiten kann ich jedoch die Grenze der Beta-Binomialverteilung (die jetzt eher einer Beta-Poisson-Verteilung ähnelt) mit einer Varianz im Exponentialfaktor der Wartezeiten ausdrücken.
Anstelle von $ 1-e ^ {- 1} $ span> suchen wir nach $$ 1- \ int e ^ {- \ lambda} p (\ lambda) \, \ text {d} \, \ lambda $$ span>.
Dieser integrale Term bezieht sich nun auf die Momenterzeugungsfunktion (mit $ t = -1 $ span>). Wenn also $ \ lambda $ span> normal verteilt ist mit $ \ mu = 1 $ span> und Varianz $ \ sigma ^ 2 $ span> dann sollten wir verwenden:
$$ 1-e ^ {- (1- \ sigma ^ 2/2)} \ quad \ text {anstelle von} \ quad 1-e ^ {- 1} $$ span>
Anwendung
Diese Würfel sind ein Spielzeugmodell. Viele Probleme im wirklichen Leben haben Variationen und nicht ganz faire Würfelsituationen.
Angenommen, Sie möchten die Wahrscheinlichkeit untersuchen, dass eine Person aufgrund einer bestimmten Kontaktzeit an einem Virus erkrankt. Man könnte Berechnungen hierfür auf der Grundlage einiger Experimente durchführen, die die Wahrscheinlichkeit einer Übertragung verifizieren (z. B. entweder theoretische Arbeiten oder Laborexperimente, bei denen die Anzahl / Häufigkeit von Übertragungen in einer gesamten Population über einen kurzen Zeitraum gemessen / bestimmt wird), und dann extrapolieren diese Übertragung auf einen ganzen Monat. Angenommen, Sie stellen fest, dass die Übertragung 1 Übertragung pro Monat und Person ist, und können dann den Schluss ziehen, dass $ 1-1 / e \ ca. 0,63 \% $ span> der Bevölkerung erhalten wird krank. Dies könnte jedoch eine Überschätzung sein, da möglicherweise nicht jeder mit der gleichen Rate krank wird / übertragen wird. Der Prozentsatz wird wahrscheinlich niedriger sein.
Dies gilt jedoch nur, wenn die Varianz sehr groß ist. Dazu muss die Verteilung von $ \ lambda $ span> sehr verzerrt sein. Denn obwohl wir es zuvor als Normalverteilung ausgedrückt haben, sind negative Werte nicht möglich und Verteilungen ohne negative Verteilungen haben normalerweise keine großen Verhältnisse $ \ sigma / \ mu $ span>, es sei denn, sie sind stark verzerrt. Eine Situation mit hohem Versatz wird unten modelliert:
Jetzt verwenden wir den MGF für eine Bernoulli-Verteilung (deren Exponent), da wir die Verteilung entweder als $ \ lambda = 0 $ span> mit der Wahrscheinlichkeit $ 1-p $ span> oder $ \ lambda = 1 / p $ span> mit der Wahrscheinlichkeit $ p $ span>.
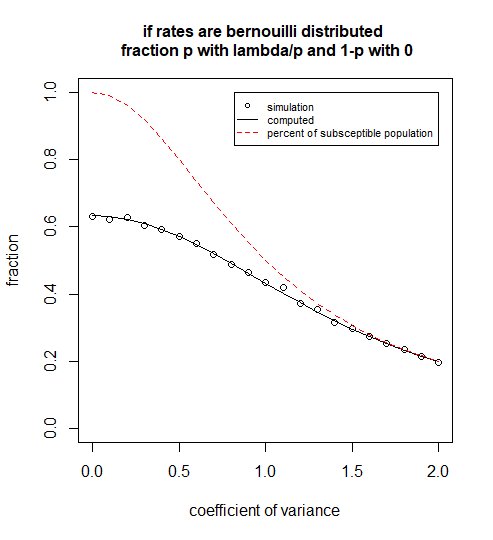
set.seed (1)
rate = 1
Zeit = 1
CV = 1
### Ergebnis für Krankheit mit variabler Rate berechnen
getick <- Funktion (Rate, CV = 0,1, Zeit = 1) {
### Abschneiden von Änderungen sd und Mittelwert, aber nicht viel, wenn der Lebenslauf klein ist
p <-1 / (CV ^ 2 + 1)
Lambda <rbinom (1,1, p) / (p) * Rate
k <-rpois (1, Lambda * Zeit)
aus <- (k>0)
aus
}}
CV <-seq (0,2,0,1)
Diagramm (-1, -1, xlim = c (0,2), ylim = c (0,1), xlab = "Varianzkoeffizient", ylab = "Bruch",
cex.main = 1, main = "wenn die Raten bernouilli verteilt sind \ n Bruchteil p mit Lambda / p und 1-p mit 0")
für (Lebenslauf im Lebenslauf) {
Punkte (Lebenslauf, Summe (replizieren (10 ^ 4, Getick (Rate = 1, Lebenslauf, Zeit = 1))) / 10 ^ 4)
}}
p <-1 / (CV ^ 2 + 1)
Linien (CV, 1- (1-p) -p * exp (-1 / p), col = 1)
Linien (CV, p, col = 2, lty = 2)
Legende (2,1, c ("Simulation", "berechnet", "Prozent der nicht wahrnehmbaren Bevölkerung"),
col = c (1,1,2), lty = c (NA, 1,2), pch = c (1, NA, NA), xjust = 1, cex = 0,7)
Die Folge ist. Angenommen, Sie haben hohe $ n $ span> und haben keine Möglichkeit, $ n $ span> Würfelwürfe zu beobachten (z. B. dauert es) zu lang), und stattdessen überprüfen Sie die Anzahl der $ n $ span> -Würfel nur für kurze Zeit für viele verschiedene Würfel. Dann könnten Sie die Anzahl der Würfel berechnen, die in dieser kurzen Zeit eine Zahl $ n $ span> gewürfelt haben, und basierend auf dieser Berechnung berechnen, was für $ n $ span> rollt. Aber Sie würden nicht wissen, wie stark die Ereignisse innerhalb der Würfel korrelieren. Es kann sein, dass Sie es mit einer hohen Wahrscheinlichkeit in einer kleinen Gruppe von Würfeln zu tun haben, anstatt mit einer gleichmäßig verteilten Wahrscheinlichkeit unter allen Würfeln.
Dieser 'Fehler' (oder man könnte sagen Vereinfachung) bezieht sich auf die Situation mit COVID-19, in der die Idee umgeht, dass wir 60% der Menschen brauchen, die immun sind, um die Herdenimmunität zu erreichen. Dies ist jedoch möglicherweise nicht der Fall. Die aktuelle Infektionsrate wird nur für eine kleine Gruppe von Menschen bestimmt. Dies kann sein, dass dies nur ein Hinweis auf die Infektiosität einer kleinen Gruppe von Menschen ist.