Es ist ungewöhnlich, dass kein Intercept passt und im Allgemeinen nicht ratsam ist - man sollte dies nur tun, wenn man weiß, dass es 0 ist, aber ich denke das (und die Tatsache, dass man die $ R ^ 2 $ für Passungen mit und ohne nicht vergleichen kann Intercept) ist bereits wirklich abgedeckt (wenn im Fall des 0-Intercept möglicherweise etwas überbewertet); Ich möchte mich auf Ihr Hauptproblem konzentrieren, nämlich, dass die angepasste Funktion positiv sein muss, obwohl ich in einem Teil meiner Antwort auf das 0-Intercept-Problem zurückkomme.

Der beste Weg, um ein Immer zu erhalten Positive Passform bedeutet, etwas zu passen, das immer positiv sein wird. Dies hängt zum Teil davon ab, welche Funktionen Sie anpassen müssen.

Wenn Ihr lineares Modell weitgehend zweckmäßig war (anstatt aus einer bekannten funktionalen Beziehung zu stammen, die beispielsweise aus einem physischen Modell stammen könnte), dann Sie könnte stattdessen mit der Protokollzeit arbeiten; Das angepasste Modell ist dann garantiert positiv in $ t $. Alternativ können Sie eher mit Geschwindigkeit als mit Zeit arbeiten. Bei linearen Anpassungen kann es jedoch zu Problemen mit kleinen Geschwindigkeiten (langen Zeiten) kommen.

Wenn Sie wissen, dass Ihre Antwort in den Prädiktoren linear ist, Sie können versuchen, eine eingeschränkte Regression anzupassen, aber bei mehrfacher Regression hängt die genaue Form, die Sie benötigen, von Ihren speziellen x ab (es gibt keine lineare Einschränkung, die für alle $ x $ funktioniert) Bit ad-hoc.

Sie können sich auch GLMs ansehen, mit denen Modelle angepasst werden können, die nicht negative Anpassungswerte aufweisen und (falls erforderlich) sogar $ E (Y) = X \ beta $ haben können .

Beispielsweise kann ein Gamma-GLM mit Identitätsverknüpfung versehen werden. Sie sollten keinen negativen Anpassungswert für eines Ihrer x erhalten (aber in einigen Fällen können Konvergenzprobleme auftreten, wenn Sie den Identitätslink erzwingen, wo er wirklich nicht passt).

Hier ist ein Beispiel: Der Datensatz cars in R, der Geschwindigkeit und Bremswege (die Antwort) aufzeichnet.

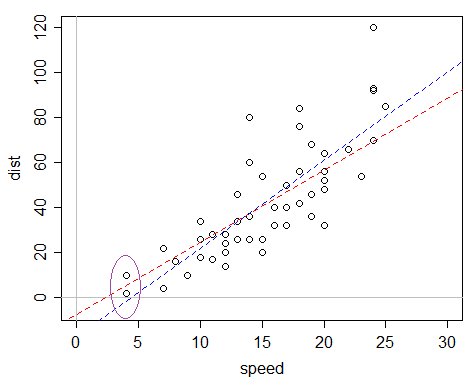
Man könnte sagen "oh, aber der Abstand für Geschwindigkeit 0 ist garantiert 0, also sollten wir den Achsenabschnitt weglassen", aber das Problem mit dieser Argumentation ist, dass das Modell auf verschiedene Weise falsch spezifiziert ist und dieses Argument nur gut funktioniert genug, wenn das Modell nicht falsch spezifiziert ist - ein lineares Modell mit einem Achsenabschnitt von 0 passt in diesem Fall überhaupt nicht gut, während eines mit einem Achsenabschnitt tatsächlich eine halbwegs anständige Annäherung ist, obwohl es nicht wirklich "korrekt" ist.

Das Problem ist, wenn Sie eine gewöhnliche lineare Regression anpassen, ist der angepasste Achsenabschnitt ziemlich negativ, was dazu führt, dass die angepassten Werte negativ sind.

Die blaue Linie entspricht der OLS-Anpassung. Der angepasste Wert für die kleinsten x-Werte im Datensatz ist negativ. Die rote Linie ist das Gamma-GLM mit Identitätsverknüpfung - während es einen negativen Achsenabschnitt hat, hat es nur positiv angepasste Werte. Dieses Modell weist eine Varianz auf, die proportional zum Mittelwert ist. Wenn Sie also feststellen, dass Ihre Daten mit zunehmender erwarteter Zeit weiter verbreitet sind, ist es möglicherweise besonders geeignet.

Dies ist also ein möglicher alternativer Ansatz, der einen Versuch wert sein kann. Es ist fast so einfach wie das Anpassen einer Regression in R.

Wenn Sie den Identitätslink nicht benötigen, können Sie andere Linkfunktionen wie den Log-Link und den inversen Link in Betracht ziehen, die sich auf die Transformationen beziehen bereits besprochen, aber ohne die Notwendigkeit einer tatsächlichen Transformation.

Da die Leute normalerweise danach fragen, ist hier der Code für meine Handlung:

  Handlung (Geschwindigkeit, Daten = Autos, xlim = c (0, 30), ylim = c (-5.120)) abline (h = 0, v = 0, col = 8) abline (glm (Geschwindigkeit, Daten = Autos, Familie = Gamma (Link = Identität)), col = 2 , lty = 2) abline (lm (dist ~ speed, data = cars), col = 4, lty = 2)  

(Die Ellipse wurde anschließend von Hand hinzugefügt, obwohl dies einfach genug ist auch in R zu tun)

Kurze Antwort auf die Frage im Titel: (fast) NIE. Im linearen Regressionsmodell $$ y = \ alpha + \ beta x + \ epsilon $$ span>, wenn Sie $ \ festlegen alpha = 0 $ span>, dann sagen Sie, dass Sie wissen, dass der erwartete Wert von $ y $ span> $ x ist = 0 $ span> ist Null. Das wissen Sie fast nie.

$ R ^ 2 $ span> wird ohne Unterbrechung höher, nicht weil das Modell besser ist, sondern weil die Definition von $ R ^ 2 $ span> verwendet ist eine andere! $ R ^ 2 $ span> ist ein Ausdruck eines Vergleichs des geschätzten Modells mit einem Standardmodell, ausgedrückt als Verringerung der Quadratsumme im Vergleich zur Quadratsumme mit dem Standardmodell . In dem Modell mit Achsenabschnitt liegt die Vergleichssumme der Quadrate um den Mittelwert. Ohne Abfangen ist es um Null! Der letzte ist normalerweise viel höher, so dass es einfacher ist, die Summe der Quadrate stark zu reduzieren.

Fazit: Lassen Sie das Intercept nicht aus dem Modell heraus (es sei denn, Sie wissen wirklich, wirklich, was Sie tun ).

BEARBEITEN (aus den Kommentaren unten): Eine Ausnahme wird an anderer Stelle in den Kommentaren erwähnt (dies ist jedoch nur scheinbar eine Ausnahme, der konstante Vektor 1 befindet sich im Spaltenraum der Entwurfsmatrix $ X $ span>. Andernfalls wie z. B. physische Beziehungen $ s = vt $ span>, bei denen es keine Konstante gibt. Aber selbst dann, wenn die Das Modell ist nur ungefähr (die Geschwindigkeit ist nicht wirklich konstant). Es ist möglicherweise besser, eine Konstante beizubehalten, auch wenn sie nicht interpretiert werden kann. Bei nichtlinearen Modellen wird dies zu einem größeren Problem.

1) Es ist niemals akzeptabel, einen Abschnitt zu unterdrücken, außer in sehr seltenen Arten von DiD-Modellen, bei denen das Ergebnis und die Prädiktoren tatsächlich berechnete Unterschiede zwischen Gruppen sind (dies ist bei Ihnen nicht der Fall).

2). Nein, tut es nicht. Dies bedeutet, dass Sie möglicherweise einen höheren Grad an interner Gültigkeit haben (z. B. das Modell passt zu den Daten), aber wahrscheinlich einen niedrigen Grad an externer Gültigkeit (z. B. das Modell) schlechte Anpassung der experimentellen Daten, die unter ähnlichen Bedingungen erhalten wurden). Dies ist im Allgemeinen eine schlechte Sache.

3) Das Unterdrücken des Abschnitts führt nicht unbedingt dazu, aber ich gehe davon aus, dass der Prädiktor kontinuierlich bewertet wurde. In vielen Situationen werden Prozessabschlusszeiten unter Verwendung einer inversen Transformation analysiert, z. $ x = 1 / t $ wobei $ t $ die Zeit ist, die benötigt wird, um einen Prozess abzuschließen. Die Umkehrung des Mittelwerts der invers transformierten Daten wird als harmonischer Mittelwert bezeichnet und repräsentiert die durchschnittliche Gesamtzeit für eine Aufgabe.

$$ \ mbox {HM} = \ frac {1} {\ mathbb {E} (x)} = \ frac {1} {\ mathbb {E} (1 / t)} $$

Sie können auch ein parametrisches Exponential- oder Gamma- oder Weibull-Time-to-Event-Modell verwenden, bei dem es sich um Modelltypen handelt, die speziell für die Vorhersage von Abschlusszeiten erstellt wurden. Diese ergeben Ergebnisse, die den invers transformierten Ergebnissen sehr ähnlich sind.

1) Das Erzwingen des Abfangens von $ 0 $ ist ratsam, wenn Sie wissen, dass es 0 ist. Alles, was Sie a priori wissen, sollten Sie in Ihrem Modell verwenden.

Eins Beispiel ist das Hubble-Modell zur Erweiterung des Universums (verwendet in Statistical Sleuth ):

$$ \ mbox {Galaxy Speed} = k (\ mbox {Entfernung von der Erde}) $$

Dieses Modell ist ziemlich grob, verwendet jedoch den 0-Achsenabschnitt als Konsequenz der Urknalltheorie: Zum Zeitpunkt $ 0 $ befindet sich die gesamte Angelegenheit an einem Ort.

Auf der anderen Seite Andererseits benötigt das Modell, das Sie beschreiben, wahrscheinlich einen Intercept-Term.

2) Möglicherweise werden Sie besser oder nicht $ R ^ 2_ {adj} $, oder Sie akzeptieren eine Nullhypothese für den Test für Intercept ist 0, aber beide sind keine Gründe, den Intercept-Term zu entfernen.

3) Um die Positivität der Antworten sicherzustellen, können Sie manchmal die Antwortvariable transformieren. Log oder sqrt funktionieren möglicherweise abhängig von Ihren Daten. Natürlich müssen Sie die Residuen überprüfen.

Es ist sinnvoll (tatsächlich notwendig), den Abschnitt in der zweiten Stufe des Engle / Granger-Kointegrationstests wegzulassen. Der Test schätzt zunächst eine kointegrierende Kandidatenbeziehung über eine Regression einer abhängigen Variablen auf eine Konstante (plus manchmal einen Trend) und die anderen nichtstationären Variablen.

In der zweiten Stufe werden die Residuen dieser Regression auf eine Einheitswurzel getestet, um zu testen, ob der Fehler tatsächlich eine Gleichgewichtsbeziehung darstellt. Da die Regression der ersten Stufe eine Konstante enthält, sind die Residuen konstruktionsbedingt Mittelwert Null. Daher benötigt der Einheitswurzeltest der zweiten Stufe keine Konstante, und tatsächlich wird die Grenzverteilung für diesen Einheitswurzeltest unter der Annahme abgeleitet, dass diese Konstante tatsächlich nicht angepasst wurde

Die einzige Möglichkeit, alle angepassten Werte auf größer als Null zu beschränken, besteht darin, einen linearen Programmieransatz zu verwenden und diesen als Einschränkung anzugeben.

Das eigentliche Problem ist, dass eine lineare Regression, die den Achsenabschnitt = 0 erzwingt, eine mathematische Inkonsistenz ist, die niemals durchgeführt werden sollte:

Es ist klar, dass wenn y = a + bx, dann Durchschnitt (y) = a + Durchschnitt (x), und tatsächlich können wir leicht erkennen, dass wir, wenn wir a und b unter Verwendung einer linearen Schätzung in Excel schätzen, die obige Beziehung erhalten.

Wenn wir jedoch willkürlich a = 0 machen, dann notwendigerweise b = Durchschnitt (y) / Durchschnitt (x). Dies steht jedoch nicht im Einklang mit dem Algorithmus für minimale Quadrate. In der Tat können Sie leicht erkennen, dass die obige Beziehung nicht erfüllt ist, wenn Sie b unter Verwendung einer linearen Schätzung in Excel schätzen

Bei Modellen mit kategorialer Kovariate ist dies ziemlich sinnvoll. In diesem Fall führt das Entfernen des Abschnitts zu einem äquivalenten Modell mit nur unterschiedlicher Parametrisierung:

  >-Daten (mtcars) > mtcars $ cyl_factor <- as.factor (mtcars $ cyl) > Zusammenfassung lm (mpg ~ cyl_factor, data = mtcars)) Aufruf: lm (Formel = mpg ~ cyl_factor, data = mtcars) Residuen: Min 1Q Median 3Q Max -5,2636 -1,8357 0,0286 1,3893 7,2364 Koeffizienten: Schätzung Std. Fehler t Wert Pr (> | t |) (Achsenabschnitt) 26,6636 0,9718 27,437 < 2e-16 *** cyl_factor6 -6,9208 1,5583 -4,441 0,000119 *** cyl_factor8 -11,5636 1,2986 -8,905 8,57e-10 *** . Codes: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1 Restlicher Standardfehler: 3,223 bei 29 FreiheitsgradenMehrfaches R-Quadrat: 0,7325, angepasstes R-Quadrat: 0,714 F-Statistik: 39,7 auf 2 und 29 DF, p-Wert: 4,979e-09> Zusammenfassung (lm (mpg ~ 0 + cyl_factor, Daten = mtcars)) Aufruf: lm (Formel = mpg ~ 0 + cyl_factor, Daten = mtcars) Residuen: Min 1Q Median 3Q Max -5,2636 -1,8357 0,0286 1,3893 7,2364 Koeffizienten: Schätzung Std. Fehler t Wert Pr (> | t |) cyl_factor4 26.6636 0.9718 27.44 < 2e-16 *** cyl_factor6 19.7429 1.2182 16.21 4.49e-16 *** cyl_factor8 15.1000 0.8614 17.53 < 2e-16 *** --- Sign. Codes: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1 Restlicher Standardfehler: 3,223 bei 29 FreiheitsgradenMehrfaches R-Quadrat: 0,9785, angepasstes R-Quadrat: 0,9763 F-Statistik: 440.9 auf 3 und 29 DF, p-Wert: < 2.2e-16  

Das zweite Beispiel führt tatsächlich dazu, dass die kategoriale Variable ein kategoriespezifischer Achsenabschnitt ist, sodass der Achsenabschnitt in Wirklichkeit nicht ist wird nicht wirklich entfernt, es scheint nur so.