Während Henry bereits eine Möglichkeit gegeben hat, die Zahl durch Zählen aller Partitionen genau zu berechnen, könnte es interessant sein, zwei ungefähre Methoden zu kennen.
Zusätzlich gibt es eine alternative exakte Berechnung basierend auf bedingten Poisson-verteilten Variablen.
Computersimulation
Sie werden nicht in der Lage sein, alle $ 12 ^ {18} $ span> -Möglichkeiten zu berechnen (und es wird nicht einfach sein, das Problem zu skalieren), aber Sie können einen Computer eine Teilmenge der möglichen Wege zufällig simulieren lassen und aus diesen Simulationen eine Verteilung erhalten.
# Funktion zum Abtasten von 18 Geburtsmonaten
# und erhalten Sie die maximale Anzahl ähnlicher Monate
Monatsbeispiel <- function () {
x <- sample (1: 12,18, replace = TRUE) # sample
n <-max (Tabelle (x)) # erhält das Maximum
return (n)
}}
# millionenfach probieren
y <-Replikat (10 ^ 6, Monatsprobe ())
# Ermitteln Sie die Frequenz mithilfe eines Histogramms
h<-hist (y, bricht = seq (-0,5,18,5,1))
Approximation mit Poissonation
Die Häufigkeit der Geburtstage in einem bestimmten Monat ist ungefähr Poisson / Binomial verteilt. Basierend darauf können wir die Wahrscheinlichkeit berechnen, dass die Anzahl der Geburtstage in einem bestimmten Monat einen bestimmten Wert nicht überschreitet, und indem wir die Potenz von zwölf nehmen, berechnen wir die Wahrscheinlichkeit, dass dies für alle zwölf Monate geschieht.
Hinweis: Hier vernachlässigen wir die Tatsache, dass die Anzahl der Geburtstage korreliert ist, sodass dies offensichtlich nicht genau ist.
# Approximation mit Poisson-Verteilung
t <- 0:18
z <-ppois (t, 1,5) ^ 12 # P (max. < = t)
dz <-diff (z) # P (max = t + 1)
Berechnung mit Bruce Levins Darstellung
In den Kommentaren hat Whuber auf das Paket pmultinom hingewiesen. Dieses Paket basiert auf Bruce Levin 1981 'Eine Darstellung für multinomiale kumulative Verteilungsfunktionen' in Ann. Statist. Band 9 . Das Ergebnis der Geburtsmonate (das genauer nach einer multinomialen Verteilung verteilt ist) wird als unabhängige Poisson-verteilte Variablen dargestellt. Im Gegensatz zu der zuvor erwähnten naiven Berechnung wird die Verteilung dieser verteilten Poisson-Variablen als bedingt angesehen, wenn die Gesamtsumme gleich $ n = 18 $ .
Also haben wir oben $$ P (X_1, X_2, \ ldots, X_ {12} \ leq 4) = P (X_1 \ leq 4) \ cdot P (X_1 \) berechnet leq 4) \ cdot \ ldots \ cdot P (X_ {12} \ leq 4) $$ span>, aber wir hätten die bedingte Wahrscheinlichkeit für die verteilten Poisson-Variablen berechnen sollen, die alle gleich oder niedriger sind als $$ P (X_1, X_2, \ ldots, X_ {12} \ leq 4 \ vert X_1 + X_2 + \ ldots + X_ {12} = 18) $$ span> welche führt einen zusätzlichen Begriff ein, der auf der Bayes-Regel basiert.
$$ P (\ forall i: X_i \ leq 4 \ vert \ sum X_i = 18) = P (\ forall i: X_i \ leq 4) \ frac {P ( \ sum X_i = 18 \ vert \ forall i: X_i \ leq 4)} {P (\ sum X_i = 18)} $$ span>
Dieser Korrekturfaktor ist das Verhältnis der Wahrscheinlichkeit, dass eine Summe abgeschnittener Poisson-verteilter Variablen gleich 18 $ P (\ sum X_i = 18 \ vert \ forall i: X_i \ leq 4) ist ) $ span> und die Wahrscheinlichkeit, dass eine Summe regulärer Poisson-verteilter Variablen gleich 18 ist, $ P (\ sum X_i = 18) $ span>. Für eine kleine Anzahl von Geburtsmonaten und Personen in der Gruppe kann diese abgeschnittene Verteilung manuell berechnet werden
# Korrekturfaktor von Bruce Levin
Korrektur <- Funktion (y) {
Nptrunc (y) [19] / dpois (18, 18)
}}
Nptrunc <- Funktion (lim) {
# verkürzte Poisson-Verteilung
ptrunc <-dpois (0: lim, 1,5) / sum (dpois (0: lim, 1,5))
## Vektor mit Wahrscheinlichkeiten
outvec <-rep (0, lim * 12 + 1)
outvec [1] <- 1
# 12 mal pro Monat zusammenfalten
für (i in 1:12) {
newvec <-rep (0, lim * 12 + 1)
für (k in 1: (lim + 1)) {
newvec <- newvec + ptrunc [k] * c (rep (0, k-1), outvec [1: (lim * 12 + 1- (k-1))])
}}
outvec <- newvec
}}
outvec
}}
z2 <-ppois (t, 1,5) ^ 12 * Vektorisieren (Korrektur) (t) # P (max< = t)
z2 [1: 2] <c (0,0)
dz2 <-diff (z2) # P (max = t + 1)
Ergebnisse
Diese Näherungen ergeben die folgenden Ergebnisse
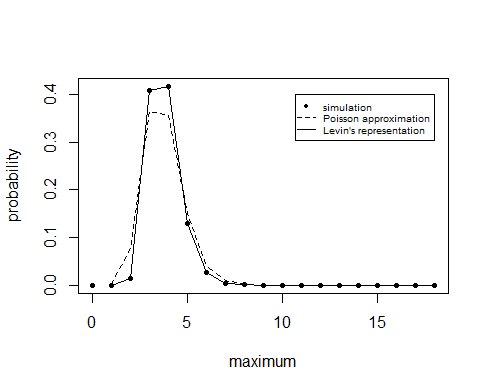
> ### Simulation
> sum (y> = 4) / 10 ^ 6
[1] 0,577536
> ### Berechnung
> 1-z [4]
[1] 0,5572514
> ### Berechnung genau
> 1-z2 [4]
[1] 0,5771871