Normalerweise würden Sie den beobachteten Wert nicht als "geschätzten Wert" bezeichnen.

Trotzdem ist der beobachtete Wert technisch gesehen eine Schätzung des Mittelwerts bei seinem bestimmten $ x $, und wenn er als Schätzung behandelt wird, wird uns dies tatsächlich mitgeteilt Sinn, in dem OLS den Mittelwert dort besser abschätzen kann.

Im Allgemeinen wird die Regression in der Situation verwendet, in der Sie, wenn Sie eine andere Stichprobe mit denselben $ x $ nehmen würden, nicht dieselben Werte für die $ y $ erhalten würden. Bei der gewöhnlichen Regression behandeln wir $ x_i $ als feste / bekannte Größen und die Antworten, $ Y_i $ als Zufallsvariablen (wobei beobachtete Werte mit $ y_i $ bezeichnet werden).

Verwenden Sie eine häufigere Notation. wir schreiben

$$ Y_i = \ alpha + \ beta x_i + \ varepsilon_i $$

Der Rauschbegriff $ \ varepsilon_i $ ist wichtig, weil die Beobachtungen nicht richtig liegen auf der Bevölkerungslinie (wenn dies der Fall wäre, wäre keine Regression erforderlich; zwei beliebige Punkte würden Ihnen die Bevölkerungslinie geben); Das Modell für $ Y $ muss die Werte berücksichtigen, die es annimmt, und in diesem Fall berücksichtigt die Verteilung des Zufallsfehlers die Abweichungen von der ('wahren') Linie.

Die Schätzung des Mittelwerts am Punkt $ x_i $ für gewöhnliche lineare Regression hat Varianz

$$ \ Big (\ frac {1} {n} + \ frac {(x_i- \ bar {x}) ^ 2} {\ sum (x_i- \ bar {x}) ^ 2} \ Big) \, \ sigma ^ 2 $$

, während die auf dem beobachteten Wert basierende Schätzung die Varianz $ \ sigma ^ 2 $ aufweist.

Es ist möglich zu zeigen, dass für $ n $ mindestens 3 $ \, \ frac {1} {n} + \ frac {(x_i- \ bar {x}) ^ 2} {\ sum (x_i- \ bar {x}) ^ 2} $ ist nicht mehr als 1 (aber es kann - und in der Praxis normalerweise - viel kleiner sein). [Wenn Sie die Anpassung auf $ x_i $ durch $ y_i $ schätzen, bleibt Ihnen auch die Frage, wie $ \ sigma $ geschätzt werden soll.]

Aber anstatt die formelle Demonstration fortzusetzen, überlegen Sie Ein Beispiel, von dem ich hoffe, dass es motivierender ist.

Lassen Sie $ v_f = \ frac {1} {n} + \ frac {(x_i- \ bar {x}) ^ 2} {\ sum ( x_i- \ bar {x}) ^ 2} $, der Faktor, mit dem die Beobachtungsvarianz multipliziert wird, um die Varianz der Anpassung bei $ x_i $ zu erhalten.

Lassen Sie uns jedoch eher auf der Skala des relativen Standardfehlers als der relativen Varianz arbeiten (dh schauen wir uns die Quadratwurzel dieser Größe an). Konfidenzintervalle für den Mittelwert bei einem bestimmten $ x_i $ sind ein Vielfaches von $ \ sqrt {v_f} $.

Also zum Beispiel. Nehmen wir die Autos -Daten in R; Dies sind 50 Beobachtungen, die in den 1920er Jahren über die Geschwindigkeit von Autos und die zum Anhalten zurückgelegten Entfernungen gesammelt wurden:

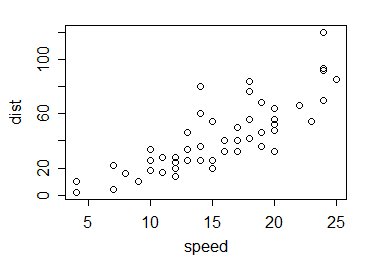
Wie verhalten sich die Werte von $ \ sqrt {v_f} $? mit 1 vergleichen? So:

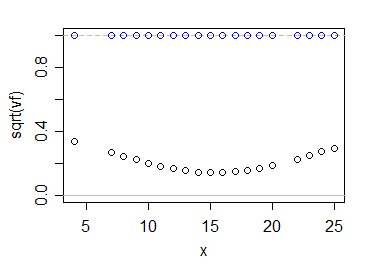
Die blauen Kreise zeigen die Vielfachen von $ \ sigma $ für Ihre Schätzung, während die schwarzen sie für die übliche Schätzung der kleinsten Quadrate anzeigen. Wie Sie sehen, macht die Verwendung der Informationen aus allen Daten unsere Unsicherheit darüber, wo der Populationsmittelwert liegt, wesentlich geringer - zumindest in diesem Fall und natürlich angesichts der Richtigkeit des linearen Modells.

Infolgedessen Wenn wir ein 95% -Konfidenzintervall für den Mittelwert für jeden Wert $ x $ (einschließlich an anderen Stellen als einer Beobachtung) zeichnen (sagen wir), sind die Grenzen des Intervalls an den verschiedenen $ x $ im Vergleich zu dem normalerweise klein Variation der Daten:

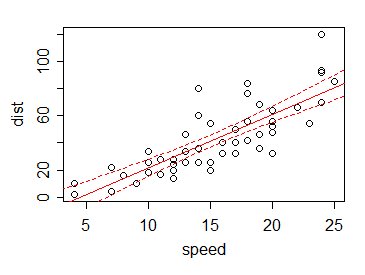
Dies ist der Vorteil des Ausleihens von Informationen aus anderen als den vorliegenden Datenwerten.

In der Tat können wir die Informationen aus anderen Werten - über die lineare Beziehung - verwenden, um gute Schätzungen des Werts an Stellen zu erhalten, an denen wir nicht einmal Daten haben. Bedenken Sie, dass es in unserem Beispiel keine Daten bei x = 5, 6 oder 21 gibt. Mit dem vorgeschlagenen Schätzer haben wir dort keine Informationen - aber mit der Regressionslinie können wir nicht nur den Mittelwert an diesen Punkten (und bei 5,5 und 12,8 und) schätzen usw.) können wir ein Intervall dafür angeben - allerdings auch eines, das von der Eignung der Linearitätsannahmen (und der konstanten Varianz der $ Y $ s und der Unabhängigkeit) abhängt.

Zunächst lautet die Regressionsgleichung:

\ begin {Gleichung} Y_i = \ alpha + \ beta X_i + \ epsilon_i \ end {Gleichung}

Es gibt einen Fehlerterm , $ \ epsilon $. Wie sich herausstellt, ist dieser Fehlerbegriff für die Beantwortung Ihrer Frage von entscheidender Bedeutung. Was genau ist der Fehlerbegriff in Ihrer Anwendung? Eine gebräuchliche Interpretation ist "der Einfluss von allem außer $ X $, der $ Y $ beeinflusst". Wenn dies Ihre Interpretation Ihres Fehlerterms ist, dann ist $ Y_i $ das beste Maß dafür, was $ Y_i $ wirklich ist.

Andererseits interpretieren wir den Fehlerterm in einigen seltenen Fällen ausschließlich als Messfehler - der Fehler, der durch den Bedienerfehler bei der Verwendung eines wissenschaftlichen Instruments oder den Fehler aufgrund der natürlich begrenzten Präzision eines Instruments verursacht wird. In diesem Fall ist der "echte" Wert von $ Y_i $ $ \ alpha + \ beta X_i $. In diesem Fall sollten Sie die OLS-Vorhersage von $ Y_i $ anstelle des tatsächlichen Werts von $ Y_i $ verwenden, wenn $ V (\ epsilon_i) >V (\ hat {\ alpha} _ {OLS} + \ hat {\ beta} _ {OLS} X_i) $ --- das heißt, wenn die Varianz des Fehlers, der durch das Ersetzen von $ \ alpha $ und $ \ beta $ durch ihre OLS-Schätzer entsteht, kleiner ist als die Varianz des Messfehlers.

Der ursprüngliche Wert ist keine Schätzung (mit Ausnahme der Tatsache, dass möglicherweise ein Messfehler vorliegt): Dies ist der Wert von Y für ein bestimmtes Subjekt (z. B. eine Person oder was auch immer). Der vorhergesagte Wert aus der Gleichung ist eine Schätzung: Es ist eine Schätzung des erwarteten Wertes von Y bei einem gegebenen Wert von X.

Lassen Sie uns dies konkretisieren:

Nehmen wir an, Y ist Gewicht und X ist Größe. Nehmen wir an, Sie messen und wiegen eine Menge Leute. Nehmen wir an, Jill ist 5'0 und 105 Pfund. Das ist ihre Größe und ihr Gewicht. Die Gleichung gibt Ihnen einen anderen vorhergesagten Gewichtswert für eine Person, die 5'0 "ist. Dies ist nicht der vorhergesagte Wert für Jill - Sie müssen ihr Gewicht nicht vorhersagen oder schätzen, Sie wissen es genau Skala. Es ist der vorhergesagte Wert einer "typischen 5'0" Person ".

Die Gleichung sollte $$ \ operatorname {E} (Y) = \ alpha + \ beta x $$ sein; das ist der erwartete Wert von $ Y $ bei dem gegebenen Wert von $ x $. Wenn Sie also mit dem richtigen & Ihres Modells genügend Beobachtungen von $ Y $ bei diesem Wert von $ x $ machen, erfahren Sie, wie hoch der Durchschnittswert von $ Y $ sein wird. Auf lange Sicht ist es besser, Vorhersagen mit diesem Durchschnitt zu treffen als mit dem beobachteten Wert.

Normalerweise wird OLS nicht durch Vergleichen der geschätzten Antwort $ \ hat {Y_i} $ mit der beobachteten Antwort $ Y_i $ motiviert. Wenn stattdessen ein neuer Satz von Werten für den Prädiktorwert $ X_ {new} $ angegeben wird, sagt das OLS-Modell voraus, wie die abhängige Variable in einem typischen Fall $ \ hat {Y} _ {new} $ lauten würde.

Der Punkt ist, dass $ \ hat {Y} _i $ normalerweise nicht als "besser" als $ Y_i $ angesehen wird, sondern eine genauere Darstellung dessen, was Sie erwarten, dass $ Y $ einen bestimmten Wert für $ X $ hat

Es gibt jedoch Situationen, in denen Sie glauben, dass $ \ hat {Y} _i $ die Wahrheit genauer widerspiegelt als $ Y_i $ (möglicherweise für einen Ausreißer, der auf eine Fehlfunktion in Ihrer Datenerfassung zurückzuführen ist). Dies hängt stark von den Details Ihrer Daten ab.

Hilft das? (Es war das, woran ich beim Lesen der Frage zuerst dachte.)

In der Statistik besagt das nach Carl Friedrich Gauss und Andrey Markov benannte Gauß-Markov-Theorem dies in einem linearen Regressionsmodell Wenn die Fehler die Erwartung Null haben und nicht korreliert sind und gleiche Varianzen aufweisen, wird der beste lineare unverzerrte Schätzer (BLAU) der Koeffizienten durch den Schätzer der gewöhnlichen kleinsten Quadrate (OLS) angegeben. Hier bedeutet "am besten" die niedrigste Varianz der Schätzung im Vergleich zu anderen unverzerrten linearen Schätzungen. Die Fehler müssen weder normal noch unabhängig und identisch verteilt sein (nur unkorreliert und homoskedastisch). Die Hypothese, dass der Schätzer unvoreingenommen ist, kann nicht verworfen werden, da ansonsten Schätzer existieren, die besser als OLS sind.

http://en.wikipedia.org/wiki/Gauss%E2%80%93Markov_theorem