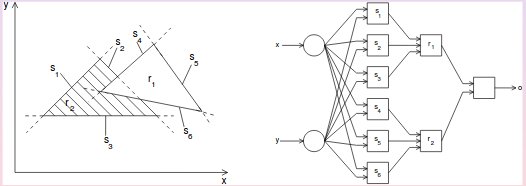
Wenn Sie ein Netzwerk mit zwei Schichten modifizierbarer Gewichte haben, können Sie beliebige konvexe Entscheidungsbereiche bilden, in denen die Neuronen der niedrigsten Ebene den Eingaberaum in Halbräume unterteilen und die zweite Schicht von Neuronen eine "UND" -Operation ausführt, um zu bestimmen, ob Sie befinden sich auf der rechten Seite der Halbräume, die den konvexen Bereich definieren. Im folgenden Diagramm können Sie auf diese Weise die Regionen r1 und r2 bilden. Wenn Sie später ein zusätzliches hinzufügen, können Sie beliebige konkave oder disjunkte Entscheidungsbereiche bilden, indem Sie die Ausgaben der Teilnetzwerke kombinieren, die die konvexen Teilbereiche definieren. Ich glaube, ich habe diesen Beweis aus Philip Wassermans Buch "Neural Computing: Theorie und Praxis" (1989) erhalten.

Sie möchten also überanpassen, ein neuronales Netzwerk mit drei verborgenen Schichten von Neuronen verwenden, eine große Anzahl von Neuronen der verborgenen Schicht in jeder Schicht verwenden, die Anzahl der Trainingsmuster minimieren (sofern die Herausforderung dies zulässt), verwenden eine Cross-Entropy-Fehlermetrik und ein Zug unter Verwendung eines globalen Optimierungsalgorithmus (z. B. simuliertes Tempern).

Dieser Ansatz würde es Ihnen ermöglichen, ein neuronales Netzwerk zu erstellen, das konvexe Unterregionen aufweist, die jedes Trainingsmuster jeder Klasse umgeben, und daher keinen Trainingssatzfehler aufweist und eine schlechte Validierungsleistung aufweist, wenn sich die Klassenverteilungen überlappen.

Beachten Sie, dass bei einer Überanpassung das Modell zu stark optimiert wird. Ein überparametrisiertes Modell (mehr Gewichte / versteckte Einheiten als erforderlich) kann immer noch eine gute Leistung erbringen, wenn die "Dateninkongruenz" nicht überminimiert wird (z. B. durch Anwenden von Regularisierung oder frühem Stoppen oder das Glück, in einem "guten" lokalen Minimum zu landen ).

Auswendiglernen

Für eine absolute Überanpassung möchten Sie ein Netzwerk, das technisch in der Lage ist, alle Beispiele zu speichern, aber grundsätzlich nicht verallgemeinerbar ist. Ich erinnere mich an eine Geschichte über jemanden, der einen Prädiktor für die Schülerleistung trainierte, der im ersten Jahr großartige Ergebnisse erzielte, im nächsten Jahr jedoch ein absoluter Misserfolg war. Dies stellte sich heraus, dass alle Spalten einer Tabelle als Features verwendet wurden, einschließlich der Spalte mit der fortlaufenden Nummer des Schülers, und das System hat es einfach geschafft zu lernen, dass z Schüler Nr. 42 erhält immer gute Noten und Schüler Nr. 43 hat schlechte Leistungen, was bis zum nächsten Jahr gut funktionierte, als ein anderer Schüler Nr. 42 war.

Für einen ersten Proof of Concept in CIFAR können Sie Folgendes tun:

1. Wählen Sie eine Teilmenge von CIFAR-Beispielen aus, für die die Farbe des Pixels in der oberen linken Ecke für jedes Bild unterschiedlich ist, und verwenden Sie diese Teilmenge als Trainingsdaten.
2. Erstellen Sie ein Netzwerk, in dem die erste Ebene nur die RGB-Werte der oberen linken Ecke auswählt und alles andere ignoriert, gefolgt von ein oder zwei vergleichsweise breiten, vollständig verbundenen Ebenen bis zur endgültigen Klassifizierungsebene.
3. Trainieren Sie Ihr System - Sie sollten 100% der Trainingsdaten und nahezu zufällige Testdaten erhalten.
ol>

Danach können Sie dies auf ein schrecklich überpassendes System für die gesamte CIFAR ausweiten:

1. Filtern Sie die eingehenden Daten nach wie vor so, dass jedes einzelne Element in den Trainingsdaten identifiziert werden kann (ein einzelnes Pixel reicht also nicht aus), aber das eigentliche Problem aus diesen Daten definitiv nicht gelöst werden kann. Vielleicht würden die ersten zehn Pixel in der oberen Reihe ausreichen; vielleicht etwas aus Metadaten - z. die Bild-ID wie im Leistungsszenario der Schüler.
2. Stellen Sie sicher, dass es keine Regularisierung jeglicher Form gibt, keine Faltungsstrukturen, die eine Unabhängigkeit der Translation implizieren, sondern nur vollständig verbundene Schichten.
3. Trainieren Sie bis zu 100% Trainingsgenauigkeit und weinen Sie über die Nutzlosigkeit des Systems.
ol>

Wenn Sie für eine sehr große Anzahl von Epochen trainieren und Ihr Netzwerk über genügend Kapazität verfügt, ist das Netzwerk im Allgemeinen überlastet. Um eine Überanpassung sicherzustellen, wählen Sie ein Netzwerk mit einer sehr hohen Kapazität aus und trainieren Sie dann für viele, viele Epochen. Verwenden Sie keine Regularisierung (z. B. Ausfall, Gewichtsabnahme usw.).

Experimente haben gezeigt, dass Netzwerke, wenn Sie lange genug trainieren, alle Eingaben im Trainingssatz speichern und eine 100% ige Genauigkeit erreichen können. Dies bedeutet jedoch nicht, dass sie bei einem Validierungssatz genau sind. Eine der wichtigsten Möglichkeiten, um Überanpassungen bei den meisten Arbeiten heutzutage zu vermeiden, besteht darin, vorzeitig anzuhalten: Wir stoppen SGD nach einer begrenzten Anzahl von Epochen. Wenn Sie also vermeiden, vorzeitig anzuhalten, und ein ausreichend großes Netzwerk verwenden, sollten Sie kein Problem damit haben, dass das Netzwerk überpasst.

Möchten Sie wirklich viel Überanpassung erzwingen? Fügen Sie dann dem Trainingssatz zusätzliche Muster mit zufällig ausgewählten Beschriftungen hinzu. Wählen Sie nun ein wirklich großes Netzwerk und trainieren Sie lange genug, um eine 100% ige Genauigkeit des Trainingssatzes zu erzielen. Die zusätzlichen zufällig markierten Stichproben behindern wahrscheinlich die Verallgemeinerung weiter und führen dazu, dass das Netzwerk beim Validierungssatz noch schlechter abschneidet.

Ihre Frage gefällt mir sehr gut.

Die Leute reden oft über Überanpassung, aber vielleicht werden nicht zu viele Leute erkennen, dass das absichtliche Entwerfen eines Überanpassungsmodells keine triviale Aufgabe ist!Besonders bei großen Datenmengen.

In der Vergangenheit war die Datengröße häufig begrenzt.Koppeln Sie beispielsweise Hunderte von Datenpunkten.Dann ist es einfach, ein überpassendes Modell zu haben.

Beim "modernen maschinellen Lernen" können die Trainingsdaten jedoch sehr groß sein, beispielsweise Millionen von Bildern. Wenn ein Modell sie überanpassen kann, wäre dies bereits eine großartige Leistung.

Meine Antwort auf Ihre Frage ist also keine leichte Aufgabe, es sei denn, Sie betrügen, indem Sie Ihre Stichprobengröße reduzieren.

Laut dem Open AI-Artikel Deep Double Descent benötigen Sie nur ein ausreichend großes neuronales Netzwerk für einen bestimmten Datensatz.Vermutlich ist der NN dadurch leistungsfähig genug, um die Trainingsdaten perfekt zu lernen, aber klein genug, um nicht den Generalisierungseffekt eines großen Netzwerks zu erzielen.Das Papier ist empirisch, daher ist der Grund, warum es funktioniert, nicht theoretisch verstanden ...

Wie Sie in der Grafik sehen können, beginnen Sie mit einem untergroßen Netzwerk, das die Daten nicht lernt.Sie können die Größe erhöhen, bis die Leistung des Testsatzes gut ist. Eine weitere Vergrößerung führt jedoch zu einer Überanpassung und einer schlechteren Leistung des Testsatzes.Schließlich treten sehr große neuronale Netze in ein anderes Regime ein, in dem der Testfehler mit der Größe immer kleiner wird.Beachten Sie, dass der Trainingsfehler (in einem anderen Diagramm dargestellt) monoton abnimmt.