Ich hatte Angst, dass dies eine kontinuierliche $ \ times $ kontinuierliche $ \ times $ kategoriale Interaktion sein würde ... OK, hier geht es weiter - zuerst erstellen wir einige Spielzeugdaten ( foo ist a binärer Prädiktor, bar und baz sind stetig, dv ist die abhängige Variable):

  set.seed (1) obs <- data.frame (foo = Probe (c ("A", "B"), Größe = 100, Ersetzen = WAHR), Balken = Probe (1: 10, Größe = 100, Ersetzen = WAHR) , baz = sample (1: 10, size = 100, replace = TRUE), dv = rnorm (100))  

Wir passen dann das Modell an und betrachten die Drei-Wege-Interaktion:

  Modell <-lm (dv ~ foo * bar * baz, Daten = obs) anova (Update (Modell, ~.-foo: bar: baz), Modell)  

Um die Interaktion zu verstehen, zeichnen wir nun die Anpassungen auf. Das Problem ist, dass wir drei unabhängige Variablen haben, also würden wir wirklich einen 4d-Plot brauchen, was ziemlich schwierig ist ;-). In unserem Fall können wir die Anpassungen einfach gegen bar und baz in zwei separaten Plots zeichnen, einen für jede Ebene von foo . Berechnen Sie zuerst die Anpassungen:

  fit.A <- data.frame (foo = "A", bar = rep (1: 10,10), baz = rep (jeweils 1: 10) = 10)) fit.A $ pred <- vorhersagen (Modell, newdata = fit.A) fit.B <- data.frame (foo = "B", bar = rep (1: 10,10), baz = rep (1: 10, jeweils = 10)) fit.B $ pred <- vorhersagen (Modell, neue Daten = fit.B)  

Zeichnen Sie als Nächstes die beiden 3D-Diagramme nebeneinander und nehmen Sie Verwenden Sie für die $ z $ -Achse dieselbe Skalierung, um die Diagramme vergleichen zu können:

  par (mfrow = c (1,2), mai = c (0,0,1,0,2) , 0) +. 02) persp (x = 1: 10, y = 1: 10, z = Matrix (fit.A $ pred, nrow = 10, ncol = 10, byrow = TRUE), xlab = "bar", ylab = "baz", zlab = "fit", main = "foo = A", zlim = c (-. 8,1.1)) persp (x = 1: 10, y = 1: 10, z = matrix (fit) .B $ pred, nrow = 10, ncol = 10, byrow = TRUE), xlab = "bar", ylab = "baz", zlab = "fit", main = "foo = B", zlim = c (-. 8,1.1))  

Ergebnis:

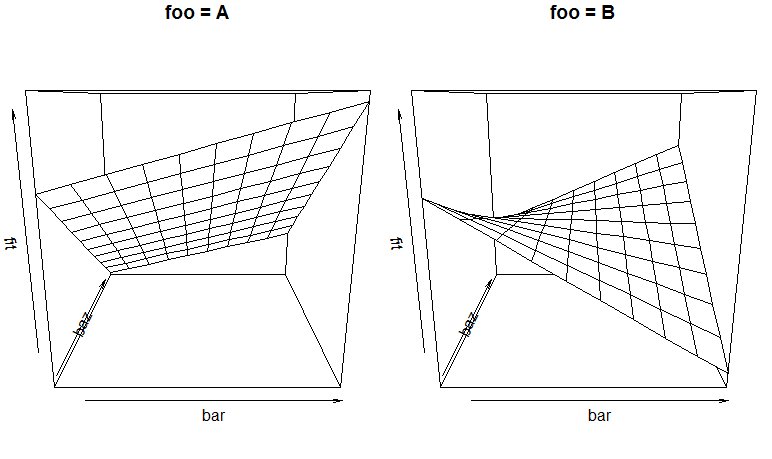
Wir sehen, wie die Art und Weise, wie die Anpassung von (beiden!) bar und baz abhängt, vom Wert von foo abhängt, und wir können Beginnen Sie, die angepasste Beziehung zu beschreiben und zu interpretieren. Ja, das ist schwer zu verdauen. Drei-Wege-Interaktionen sind immer ... Statistiken sind einfach, Interpretationen sind schwierig ...

Sehen Sie sich ? Persp an, um zu sehen, wie Sie das Diagramm verschönern können. Das Durchsuchen der R Graph Gallery kann ebenfalls inspirierend sein.

+1 zu den obigen Kommentaren zur grafischen Darstellung der Interaktion.

Ein erster Ansatz zum Nachdenken über eine Drei-Wege-Interaktion besteht darin, dass das in der Interaktion zwischen A und B enthaltene Ergebnismuster davon abhängt das Niveau / der Wert von C. Das Folgende ist in einem linearen Regressionsrahmen gerahmt, aber konzeptionell ähnlich wie z logistische Regression.

Dies setzt natürlich voraus, dass Sie mit wechselseitigen Interaktionen zufrieden sind :-)

Nehmen wir an, es gibt drei Prädiktoren: A (kontinuierlich), B. (kategorisch) und C (kategorisch).

Eine wechselseitige A * B-Interaktion würde anzeigen, dass die Steigung von A (in Bezug auf das Ergebnis) von der Ebene von B abhängt, zu der eine Person gehört.

In diesem Zusammenhang würde eine Drei-Wege-A * B * C-Wechselwirkung anzeigen, dass die A * B-Wechselwirkung (zuvor diskutierte unterschiedliche Steigungen von A auf das Ergebnis nach Gruppe von B) von der Gruppe von C bis abhängt welches gehört ...

Die Dinge sind viel komplexer, wenn es zwei kontinuierliche / ordinale Prädiktoren in der Interaktion gibt (normalerweise zu komplex, um sie sich vorzustellen: Ich wäre interessiert, die Meinungen anderer dazu zu hören.)

Oft ist es hilfreich, die Beziehungen zu zeichnen und zu sehen, wie sich die Dinge ändern, wenn Sie eine der Variablen ändern. Einige Tools in R, die bei diesen Plots helfen, sind die Funktionen Predict.Plot und TkPredict im TeachingDemos-Paket.