Ich denke, das ist ein sehr schönes Problem. Wenn ich die Notation leicht ändern darf ...

Das Problem

Lassen Sie $ \ quad W \ sim N (\ mu_0, \ sigma_0 ^ 2), \ quad X_1 \ sim N (\ mu_1, \ sigma_1 ^ 2), \ quad X_2 \ sim N (\ mu_2, \ sigma_2 ^ 2) $

bezeichnen unabhängige Zufallsvariablen und lassen $ c $ bezeichnen eine Konstante.

Suchen Sie das PDF von $ Z $, wobei:

$$ Z = \ begin {Fälle} W + X_1 & \ text {if} W \ leq c \\ W + X_2 & \ text {if} W > c \ end {Fälle} $$

Lösung

Um dies zu lösen, müssen wir 2 Probleme lösen.

Finde $ h_1 (z) $: das PDF von $ (W + X_1) \, \ big | \, (W \ leq c) \ quad $ ( dh über Normal + Normal abgeschnitten)

1. Finden Sie $ h_2 (z) $: the pdf von $ (W + X_2) \, \ big | \, (W > c) \ quad $ ( dh abgeschnitten unter Normal + Normal)

ol>

Dann sagen wir das PDF von $ Z $ $ h (z) $ ist die Komponentenmischung:

$$ h (z) \, = \, P (W \ leq c) * h_1 (z) \ quad + \ quad P (W>c ) * h_2 (z) $$

---

Lösung: Teil 1

$ \ rightarrow $ Das PDF der Summe von a über Normal und Normal abgeschnitten

Wenn $ W $ OBEN bei $ c $ abgeschnitten ist, ... dann das gemeinsame PDF von $ (W \ big | (W \ leq c) , X_1) $, sagen wir $ f_1 (w, x_1; c) $, ist aus Unabhängigkeit einfach das Produkt der jeweiligen einzelnen PDFs ... dh $ f_1 (w, x_1; c) = \ frac {f_w (w)} {P (W<c)} * f_ {x_1} (x_1) $:



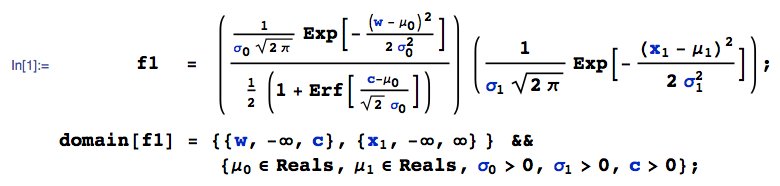
Als nächstes transformiere $ (W. , X_1) \ rechter Pfeil (Z = W + X_1, V = X_1) $. Hier ist das gemeinsame PDF von $ (Z, V) $, sagen wir $ g_1 (z, v) $:



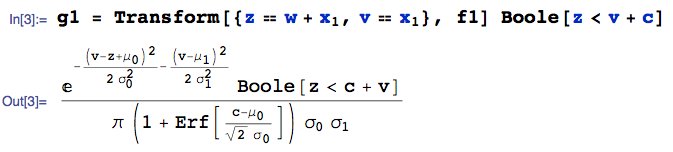
wobei:

• Ich verwende die Funktion Transform im Paket mathStatica , damit Mathematica das Wesentliche erledigt -gritties.

• Beachten Sie, dass die Transformationsgleichung $ (Z = W + X_1, V = X_1) $ eine Abhängigkeit zwischen $ Z $ und $ V $ induziert. Insbesondere, da $ Z = V + W $ und $ W < c $, folgt, dass $ Z < V + c $. Diese wichtige Einschränkung wird mit der obigen Anweisung Boole [blah] eingegeben.

• Erf [.] bezeichnet die Fehlerfunktion

Wir suchen das marginale PDF von $ Z = W + X_1 $, sagen wir $ h_1 (z) $, das heißt:

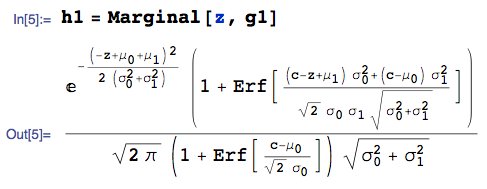
... in der realen Zeile definiert. Damit ist Teil 1 abgeschlossen.

Lösung: Teil 2

$ \ rightarrow $ Das PDF der Summe eines unten abgeschnittenen Normal und normal

Wenn $ W $ UNTEN bei $ c $ abgeschnitten ist, ... dann das gemeinsame PDF von $ (W \ big | (W > c), X_2) $ Angenommen, $ f_2 (w, x_2; c) $ ist aus Unabhängigkeit einfach das Produkt der jeweiligen einzelnen PDFs ... dh $ f_2 (w, x_2; c) = \ frac {f_w (w)} {P (W>c)} * f_ {x_2} (x_2) $:

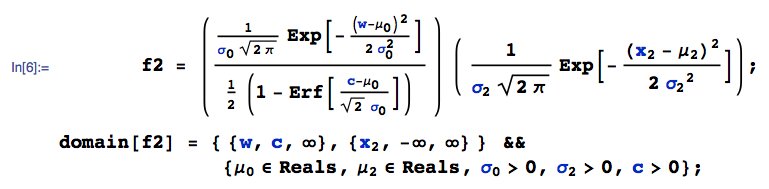
Als nächstes transformiere $ (W, X_2) \ rechter Pfeil (Z = W + X_2, V = X_2) $. Hier ist das gemeinsame PDF von $ (Z, V) $, sagen wir $ g_2 (z, v) $:

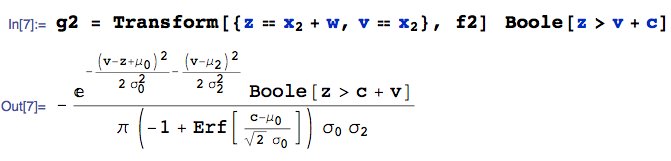
• Beachten Sie, dass die Transformationsgleichung $ (Z = W + X_2, V = X_2) $ eine Abhängigkeit zwischen $ Z $ und $ V $ induziert. Insbesondere folgt, da $ Z = V + W $ und $ W > c $, dass $ Z > V + c $. Diese wichtige Einschränkung wird mit der obigen Anweisung Boole [blah] eingegeben.

Wir suchen das marginale PDF von $ Z = W + X_2 $, sagen wir $ h_2 ( z) $, dh:

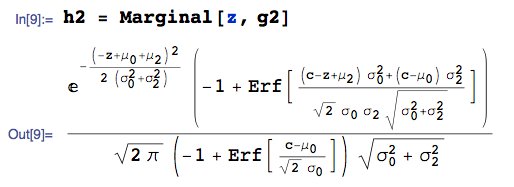
... definiert in der realen Zeile. Damit ist Teil 2 abgeschlossen.

Der Komponentenmix

Alle erforderlichen Teile des Puzzles sind jetzt vorhanden. Um dies explizit zu machen, wenn $ W \ sim N (\ mu_0, \ sigma_0 ^ 2) $ mit pdf $ f (w) $:

... dann ist $ P (W<c) $:

Denken Sie daran, dass das PDF von $ Z $ lautet:

$$ h (z) \, = \, P (W \ leq c) * h_1 (z) \ quad + \ quad P (W>c) * h_2 (z) $$

... was explizit lautet:

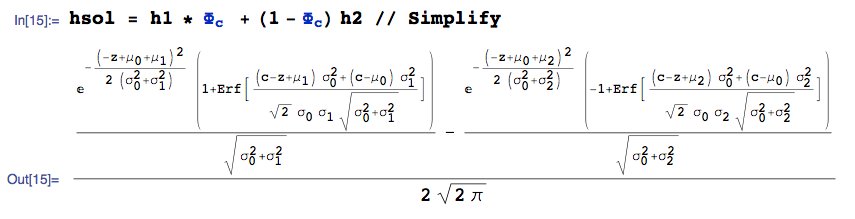
wobei $ Z $ in der reellen Linie definiert ist. Alles erledigt.

Monte-Carlo-Prüfung

Es ist immer eine gute Idee, die symbolische Arbeit mit alternativen Methoden zu überprüfen. Hier ist eine kurze Monte-Carlo-Überprüfung, wenn:

$ \ text {params} = \ left \ {\ mu _0 \ bis 16, \ mu _1 \ bis 3, \ mu _2 \ bis 2, \ sigma _0 \ bis 6, \ sigma _1 \ bis 0.1, \ sigma _2 \ bis 2, c \ bis 12 \ rechts \} $

Das folgende Diagramm vergleicht:

• eine Monte-Carlo-Simulation des PDF von $ Z $ (schnörkellose BLAUE Kurve) zu der oben abgeleiteten
• theoretischen Lösung (gestrichelte ROTE Kurve)

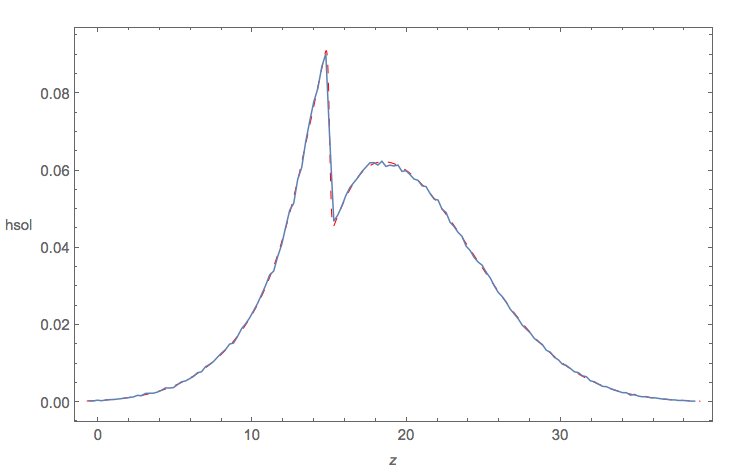
Sieht gut aus :) Unterschiedliche Parameteroptionen können natürlich zu sehr unterschiedlich geformten Ergebnissen führen.

Mittelwert von $ Z $ stark>

Paulius Šarka fragt: "Hat der Mittelwert von Z eine analytische Form?"

Ja - es ist am einfachsten, dies abzuleiten aus:

$$ Z = \ begin {Fälle} W + X_1 & \ text {if} W \ leq c \\ W + X_2 & \ text {if} W >c \ end {Fälle} $$

... Daraus folgt:

$$ E [Z] = P (W \ leq c) \ big (E [W \ big | W \ leq c] + \ mu_1 \ big) \ quad + \ quad P (W>c) \ big (E [W \ big | W > c] + \ mu_2 \ big) $$

, was die Lösung in geschlossener Form ergibt:

$$ E. [ Z] \ quad = \ quad \ mu_0 \, + \, P (W \ leq c) \ mu_1 \, + \, P (W > c) \ mu_2 $$